
理查德·费曼(Richard Feynman)是美国理论物理学家,与美国物理学家朱利安·施翁格(Julian Schwinger)和日本物理学家友永信一郎(Shinichiro Tomonaga)共同获得1965年诺贝尔物理学奖。他是世界上最著名的科学家之一。在1999年英国《物理世界》杂志对全球130位顶尖物理学家的民意调查中,他被评为有史以来十大最伟大的物理学家之一。

图1,1965年获得诺贝尔奖后,费曼在欧洲核子研究中心的研讨会上发言
费曼对物理学做出了一些基础性的贡献。这些包括量子力学的路径积分公式,量子电动力学理论(描述亚原子粒子行为的图形表示,著名的费曼图),以及液氦的超流体性的理论解释。他也是量子计算领域的先驱,引入了纳米技术的概念,以及其他许多东西。费曼也是一位著名的物理学科普者。
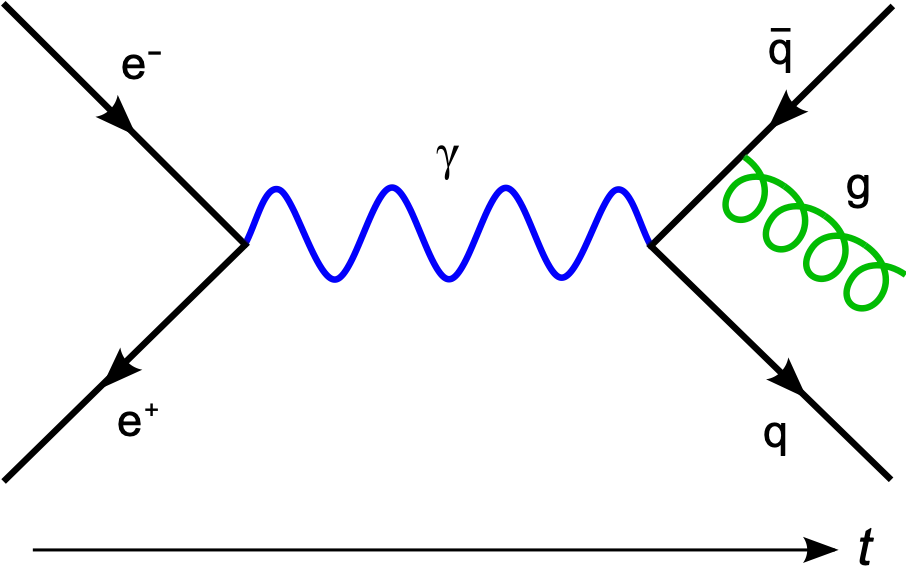
图2,费曼图的一个例子。在这里,一个电子(e⁻)和一个正电子(e⁺)湮灭,产生一个光子γ。光子就变成了一个夸克-反夸克对,之后,反夸克辐射出一个胶子g。
费曼曾经这样描述他对科学的看法:
如果你希望科学能给出关于我们是什么的所有答案,我们要去哪里,宇宙的意义是什么……你很容易幻灭,然后寻找一个神秘的答案……我们正在探索,试图尽可能多地了解这个世界。人们会问我,你在寻找终极物理定律吗?不,我没有,我只是想多了解一下这个世界。如果事实证明有一个终极法则可以解释一切,那就顺其自然吧,这将是一个非常好的发现。
如果事实证明它像洋葱,有数百万层,那么它就是这样的。但不管结果如何,这都是自然的,她会变成她自己的样子!因此,我们不应该预先决定我们将要发现的是什么,除非尝试去发现更多。如果你认为你能得到一些深奥的哲学问题的答案,那你可能错了——你可能无法通过更多地了解自然的特性来得到这个特定问题的答案。但我不这么看,我对科学的兴趣是要更多地了解这个世界,我发现的越多越好。——理查德·费曼
费曼微积分的笔记本
20世纪30年代初,费曼还在法洛克威高中读书时,根据一本名为《实用人士微积分》(Calculus for the Practical Man)的书,他整理了一套手写笔记。在那个时候,对一个高中生来说,有一个微积分老师是很不寻常的。费曼的笔记与那本书紧密相连,他从头到尾逐字逐句地阅读那本书。
正如《今日物理》所指出的那样,“费曼的微积分笔记说明了这位著名物理学家的决定性特质之一,他永不满足的好奇心……当他发现一门令他感兴趣的学科时,他不会坐等合适的老师出现,他一定会自己掌握它。”

图3,费曼的笔记本。
本部分紧跟着费曼、莱顿(Leighton)和桑兹( Sands)所著的书,以下将其称为FLR。在这本书中,费曼描述了一种快速计算复杂的多乘积函数的导数的聪明方法。
简单函数的导数
要理解费曼方法,我们只需要知道以下类型的导数:
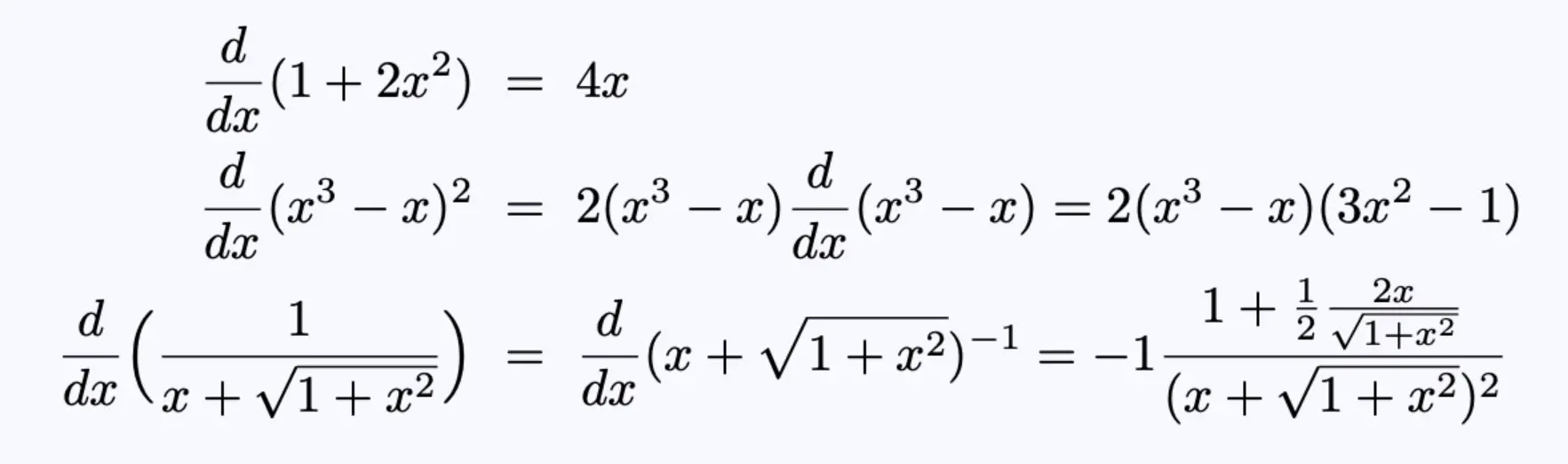
方程1,费曼算法中使用的简单导数的例子。
更复杂函数的导数
这里将用到的FRS中的例子是:
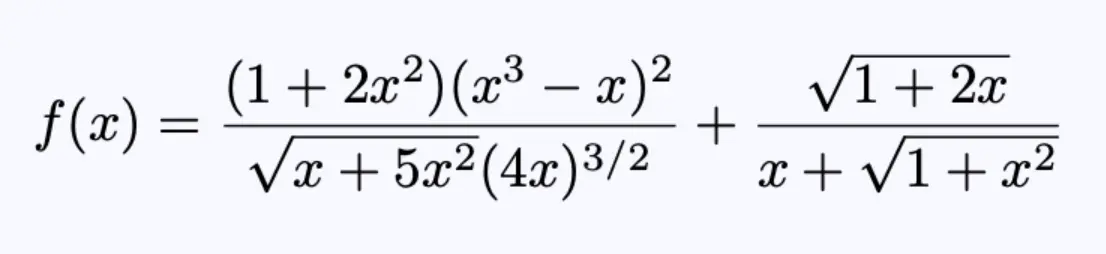
方程2,待微分函数。
跟随费曼,第一步是重复f(x)中的两项,每项乘以一个尚未确定的表达式,如下所示:
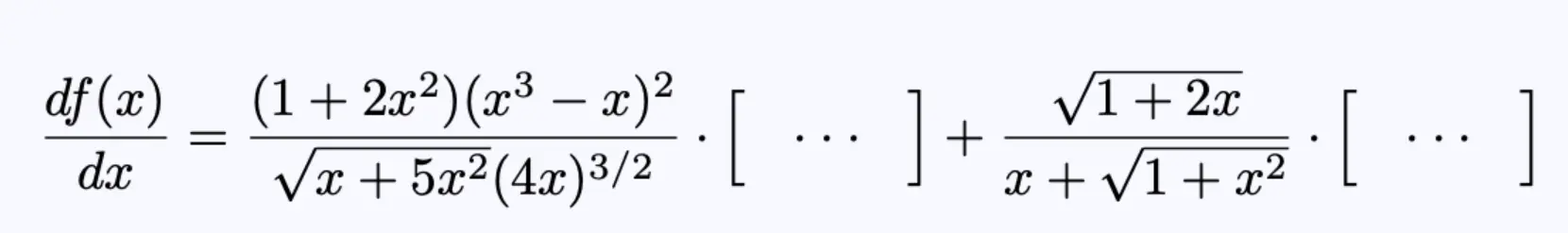
方程3,微分f(x)的第一步。
这两项都包含一个分子因式的乘积和另一个分母因式的乘积。为方便起见,我们可以将表达式写成:
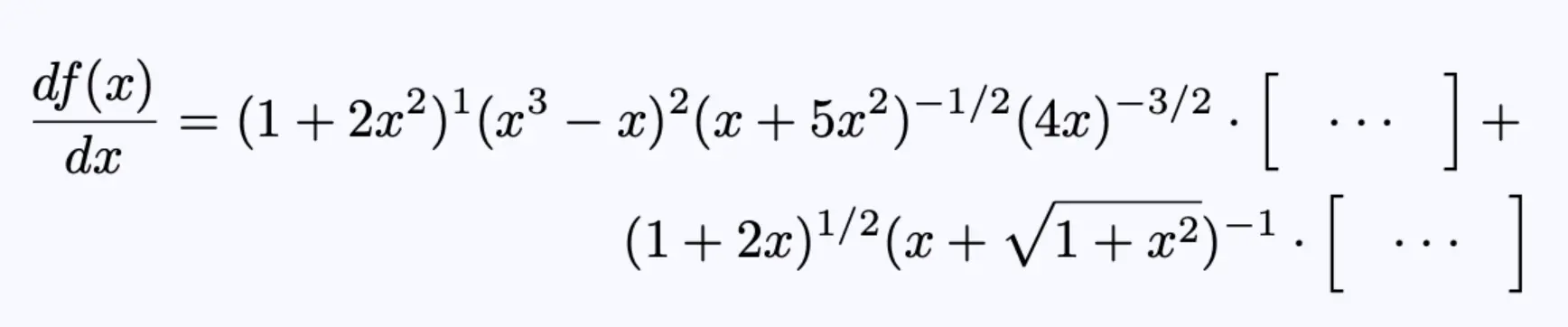
方程4,用更方便的方式写方程3。
括号内的表达式是函数的和。为了得到这些和的每一项,我们应用下面的3步算法。例如,考虑第一个因式,即(1+2x²)这三个步骤是:
这个因式变成了两个括号中第一项的分母
这个因式的指数,也就是1,变成了第一个括号内第一项的前因式
这个因式的导数变成了第一个括号内第一项的分子
下面的原理图使算法更加具体:
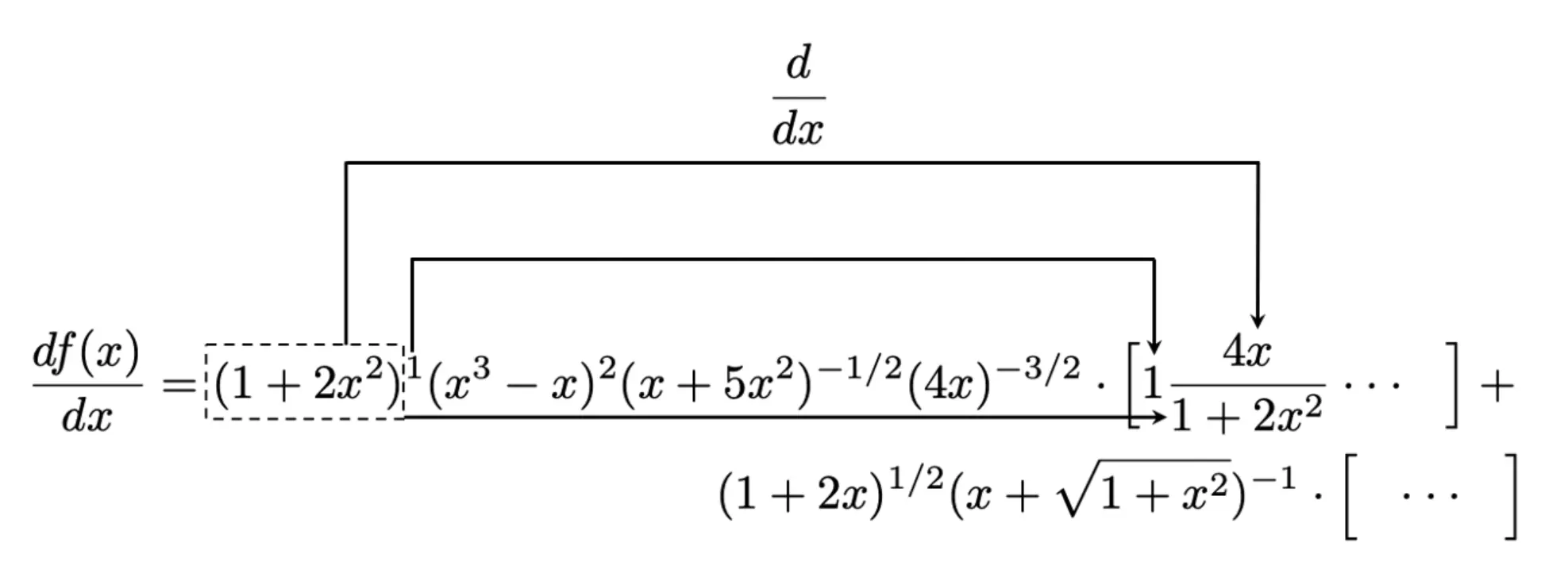
方程5,将算法应用到f(x)第一项的第一个因式上。
现在,将算法应用到f(x)第一项的第二个因式上:
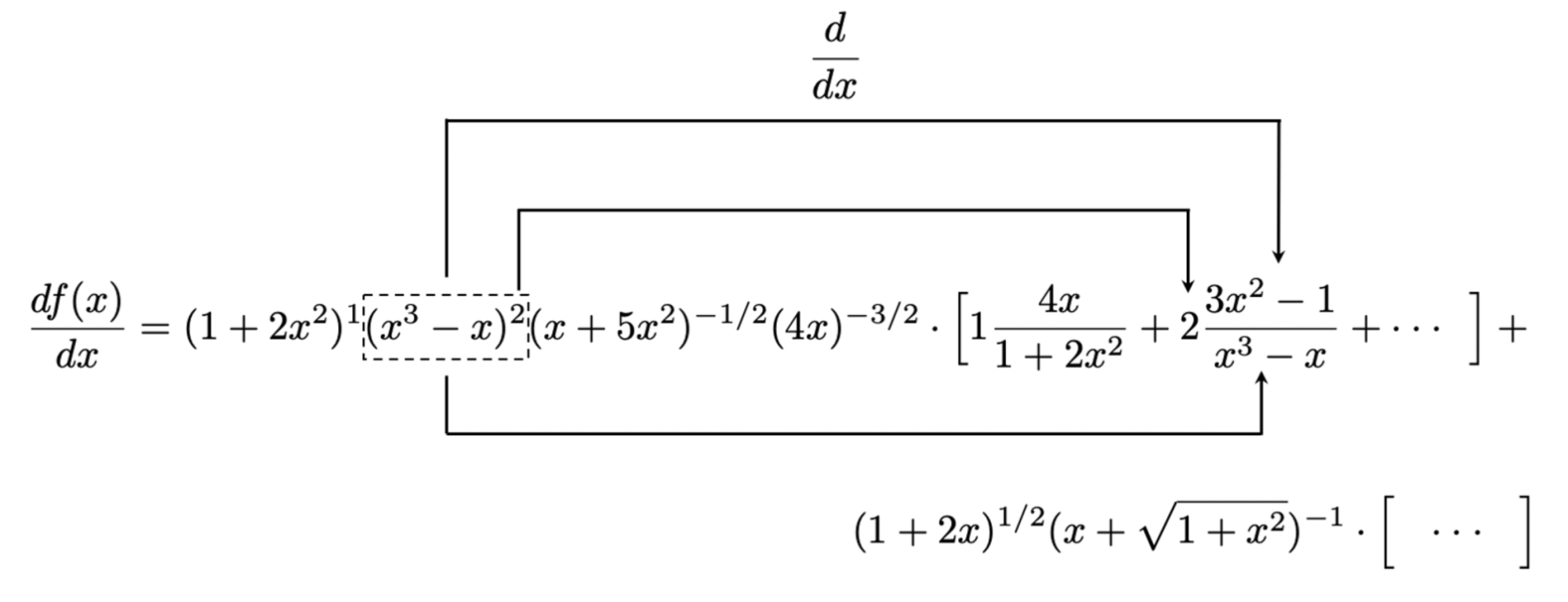
方程6,将算法应用于第一项的第二个因式。
将该算法应用于所有项,得到f(x)的导数,即:
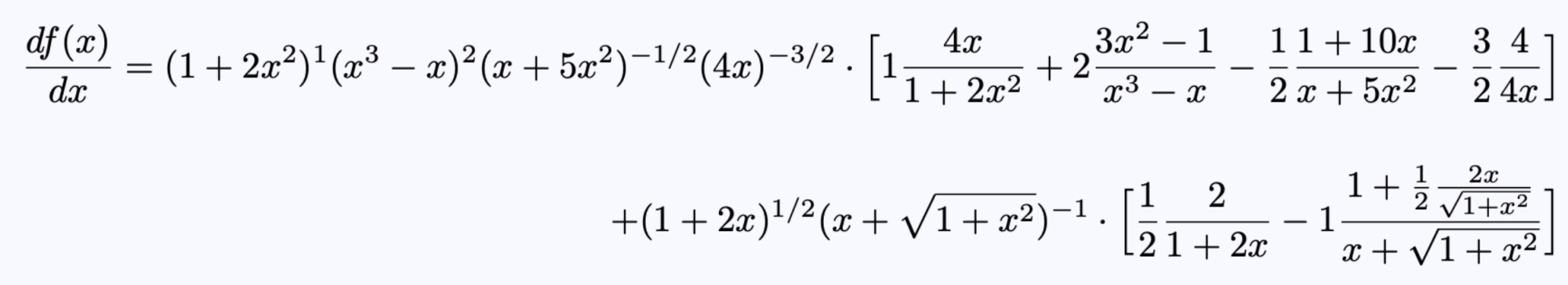
方程7,将算法应用到整个表达式,得到最终结果。
算法的普遍化
方程2是两项的和,每一项的形式如下:
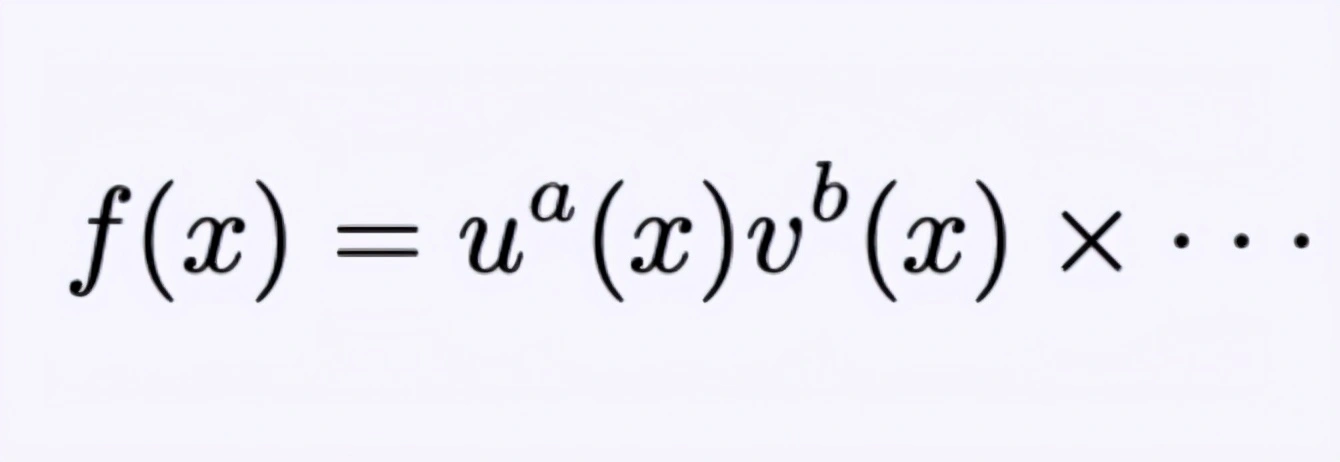
方程8,方程2中两项各一项的形式。
方程8的导数的一般形式为:
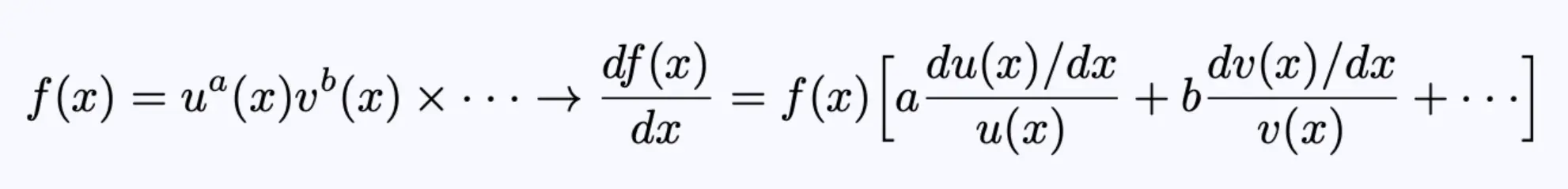
方程9,对方程7的推广。
想了解更多精彩内容,快来关注老胡说科学
转载请超链接注明:头条资讯 » 理查德·费曼如何求复杂函数的导数的?非常聪明的求导技巧
免责声明
:非本网注明原创的信息,皆为程序自动获取互联网,目的在于传递更多信息,并不代表本网赞同其观点和对其真实性负责;如此页面有侵犯到您的权益,请给站长发送邮件,并提供相关证明(版权证明、身份证正反面、侵权链接),站长将在收到邮件24小时内删除。