在爱琴海区域,萨莫斯岛和米利都相距不远,然而萨莫斯岛的风气却要保守得多,一种不太严格的宗教在这里盛行,这导致了与米利都风格迥异的哲学学派的兴起。
这种新哲学的先驱是萨莫斯的毕达哥拉斯(Pythagoras)(大约公元前580-500年)。
毕达哥拉斯的前期生涯跌宕起伏。他成年后就离开了萨摩斯岛,去了埃及,在那里他生活了十年并学习了埃及数学,后来,他成为埃及波斯人的俘虏,并被俘虏到巴比伦,在那里他又住了五年,并掌握了更高级的数学。

毕达哥拉斯乘船返回故乡至他背井离乡已有19年的时间,回到爱琴海后,他仰慕泰勒斯,就到了米利都学习,他异常聪明,在泰勒斯的指导下,解决了许多数学问题。
但是,保守的萨摩斯人仍然不能接受毕达哥拉斯的想法,因此他不得不再次横渡大海,来到意大利南部的克罗内托,在那里定居下来,娶了一个妻子,生了孩子,并招收了许多的徒弟,成立了辉煌的毕达哥拉斯学派。
毕达哥拉斯本人创造了“哲学”和“数学”这两个词,前者的意思是“爱好智慧的人”,后者的意思是“学习知识”。

其中,他证明了三角形的内角之和等于180°;他证明了,如果用砖铺地面,则只能使用三种规则的多边形砖(即规则的三角形,规则的四边形和规则的六边形)才能精确地覆盖地面,他甚至发现了黄金分割。

他还发现规则的多面体只有五种类型,即:规则的4、6、8、12和20面体。后来他还发明了影响力巨大的毕达哥拉斯定理(即勾股定理)并用演绎法给与证明。
毕达哥拉斯对勾股定理是如此喜爱,以至于用诗歌来描述他的这一发现:
斜边的平方,
如果我没有算错的话,
等于其他两条边的,
平方之和。

相比于毕达哥拉斯几何方面的卓越成就,他在代数领域也硕果累累。
毕达哥拉斯发现了奇数,偶数,素数,合数,完美数,亲和数和平方数。
所谓的完美数是一个等于其所有因子之和的数字,例如6和28,因为
6 = 1十2十3;
28 = 1十2十4十7十14。
亲和数是指这样的一对数字,其中任何一个都是另一个真因子的和,例如220和284。
后人甚至为亲和数增加了不少的神秘色彩,让亲和数在魔法及占星术方面有了广泛的应用。

但是亲和数的条件太过苛刻,一直到两千多年以后.第二对亲和数(17926,18416)才由法国数学家费尔马找到,费尔马的朋友笛卡尔则找到了第三对亲和数(9363584和9437056)。
到了18世纪中期,亲和数有了代数运算基础,欧拉根据运算,一下子发现了58对亲和数。欧拉采用了新的算法,将亲和数划分为五种类型加以讨论,解开了令人2500多年的难题,使人感到无比惊艳。
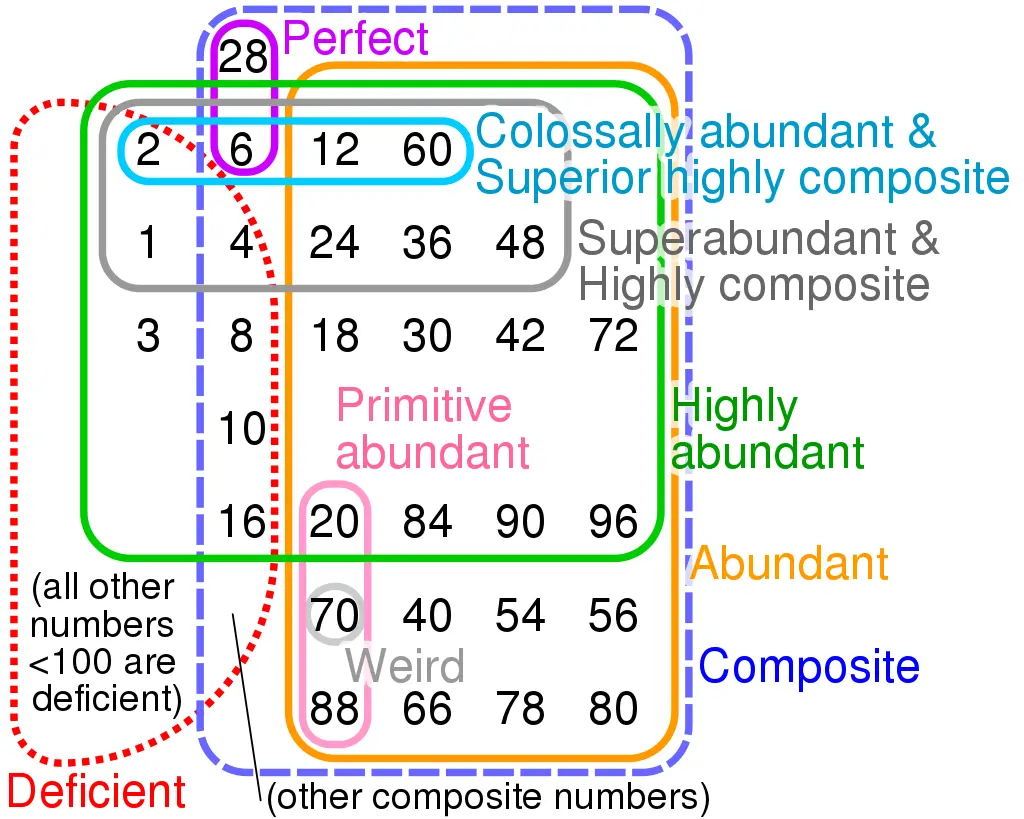
(欧拉数图)
到了现代,运用科学计算机运算.数学家们已经发现了一千多对的亲和数。不过第二小的一对(1184,1210)却是在19世纪后期才由一位16岁的意大利男孩帕格尼尼找到的。
毕达哥拉斯的成就是如此之高,以至于学派内的人,都把他看做神明一般,发展到后来,毕达哥拉斯说的话几乎成了圣旨,成了绝对正确不容置疑的东西。
毕达哥拉斯晚年,对他的造神运动已然达到高潮,这也为后面的第一次数学危机埋下了伏笔。

转载请超链接注明:头条资讯 » 这位天才发现了素数、完美数和亲和数,证明三角形内角和是180
免责声明
:非本网注明原创的信息,皆为程序自动获取互联网,目的在于传递更多信息,并不代表本网赞同其观点和对其真实性负责;如此页面有侵犯到您的权益,请给站长发送邮件,并提供相关证明(版权证明、身份证正反面、侵权链接),站长将在收到邮件24小时内删除。