当你第一次遇到“虚数”时,你是否会想,我什么时候才能用它?虚数以及由它组成的复数是非常有用的。它对物理学、工程学、数论和几何都有深远的影响。它们是进入奇异数字系统世界的第一步,其中一些数字系统被提出作为我们物理世界的模型。让我们来看看它是如何扎根于我们已知的数字系统,但与此同时,却不像我们想象的那样。
实数是我们最熟悉的数学对象,它们都是可以用十进制表示的数字,如5、8.2、-13.712、0、10.33333…。我们可以对实数进行加、减、乘、除运算,在日常生活中,我们都用实数来回答问题。但是实数并不足以解决所有的数学问题。
在16世纪,方程求解大师吉罗拉莫·卡达诺试图解多项式方程。他毫不费力地解出 x^2-8x+12=0这样的方程,因为很容易找到两个和为8,积为12的数(2和6)。这意味着可以将这个多项式表示为两个因子的乘积(x-2)(x-6)。
但对于x^2-3x+10=0这样的方程就不那么容易了。找到两个和为3积为10的数似乎是不可能的。然而,卡达诺发现,如果给-1的平方根赋值,就能找到这样的数。这是一个令人不安的发现。当平方一个实数时,结果永远不会是负数。这意味着没有实数的平方可以等于-1。卡达诺用-1的平方根来解他的实数方程,但-1的平方根不是实数。
卡达诺非常谨慎地对待这些非实数,他惊讶地发现,它们遵循着许多与实数相同的规则。卡达诺的发现导致了复数的发展,这是实数的一个强大而有效的扩展。
复数由实部和虚部组成。它们的形式是a + bi,其中a和b都是实数,i被称为虚单位。乍一看,它们似乎很奇怪,但我们很快就会发现复数的加减乘除运算与实数的运算是一样的。
要加减复数,只需将实部和虚部合并,就像这样:
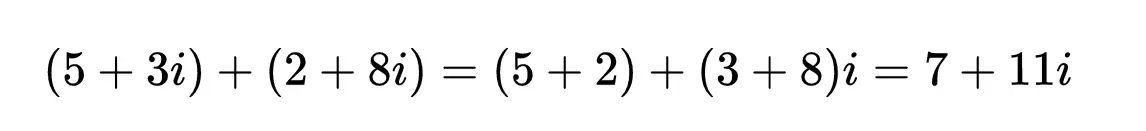
复数的乘法与实数的分配律是一样的。例如,当2和5 + i相乘时:
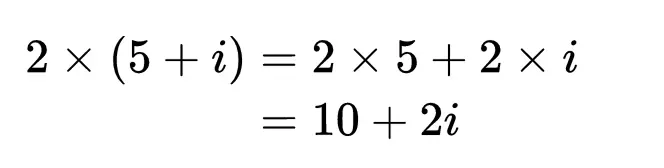
要将2 + 3i和5 + i相乘,只需应用两次分配律:
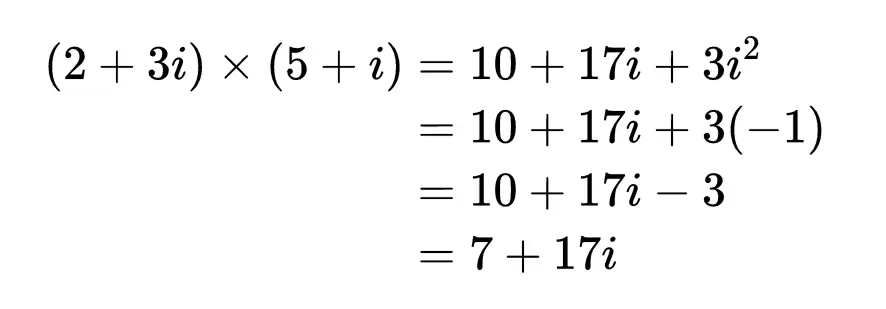
两个复数相乘仍然得到复数,这说明复数就有“闭包”性质。复数的乘法是符合交换律的。我们可以把复数相乘,但是怎么做除法呢?关键在于理解除法和乘法之间的关系。
在学校,老师可能讲过,没有除法,只有倒数的乘法。一个非零实数a的倒数是1/a。但当你开始考虑像1/i这样的数字时,它的含义可能不是很清楚,但i的倒数是与i相乘得到1的数。你可能会有点惊讶,这个数字是-i !
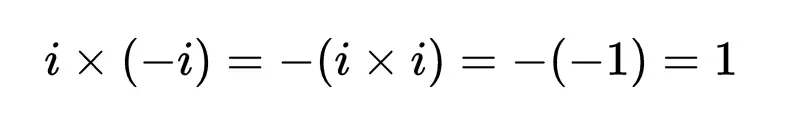
使用i×i= –1这一事实,以及实数和复数的一些重要性质,我们看到i × (-i) = 1,那么-i就是i的倒数。这意味着如果我们想用i除一个数,我们可以用-i来代替作乘法。
对于其他复数,计算可能会有点困难,但是倒数的思想仍然有效。例如,要计算(1+2i)/(3+4i),我们需要找到3+ 4i的倒数,为此,我们将使用复数的“共轭”技巧,也就是改变其虚部的符号时得到的数。
当复数3 + 4i乘以它的共轭3 - 4i会发生什么?(3+4i)×(3−4i)
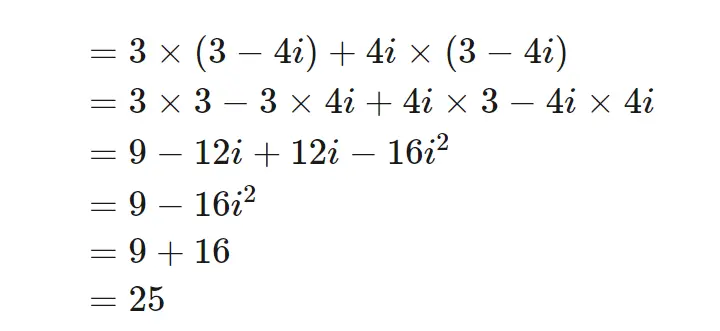
复数与其共轭的乘积是实数。共轭的这个性质帮助我们计算任何复数的倒数。由于(3 + 4i) × (3 - 4i) = 25,方程两边同时除以25,做一些代数运算:
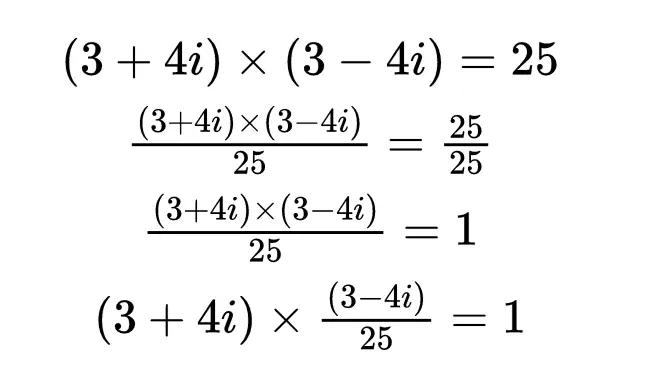
请点击输入图片描述
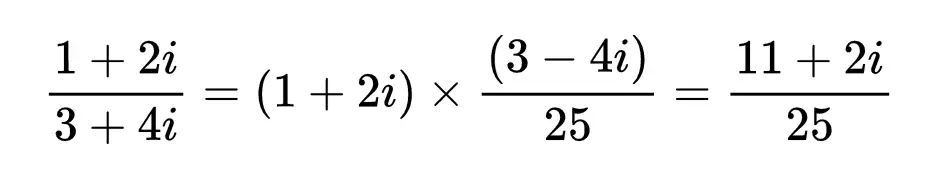
引入了这一新的非实数i(虚单位),开启了一个全新的数学世界。这是一个奇怪的世界,平方可以是负的,但它的结构与我们所熟悉的实数非常相似。而这种对实数的扩展仅仅是个开始。
1843年,威廉·罗文·汉密尔顿想象了一个世界,其中有许多不同的“虚单位”,并在此过程中发现了四元数。四元数的结构与复数相似,但有额外的-1的平方根,汉密尔顿称之为j和k。每个四元数的形式为a + bi + cj +dk,其中a, b, c和d是实数, i^2=j^2=k^2=-1。你可能认为任何人都可以发明一个新的数字系统,但重要的是要问它是否具有我们想要的结构和属性。例如,该系统在乘法下是封闭的吗?
为了确保四元数具有这些属性(封闭性,四元数相乘仍然是四元数),汉密尔顿必须弄清楚如何处理i × j。所有四元数需要看起来像a + bi + cj +dk,但i × j并不像。当我们第一次将两个复数相乘时,我们遇到了类似的问题,结果中有一个i × i项,但我们可以利用 i^2=-1这一事实来将这个数字转换成正确的复数形式(从而保证了复数在乘法下封闭)。但是如果i^2=−1i × j呢?
汉密尔顿自己也在努力思考这个问题,当灵感终于到来的时候,他把自己的见解刻在了桥的石头上:
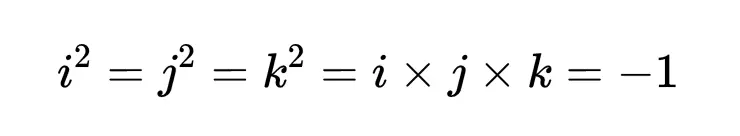
来自世界各地的人们仍然会访问都柏林的布鲁姆桥来分享这一数学发现的时刻。
汉密尔顿在虚单位i、j和k之间的著名关系允许我们对四元数进行乘法和除法,并得到我们最期望的结果。从i × j × k = -1开始,我们在方程的两边乘以k并化简。
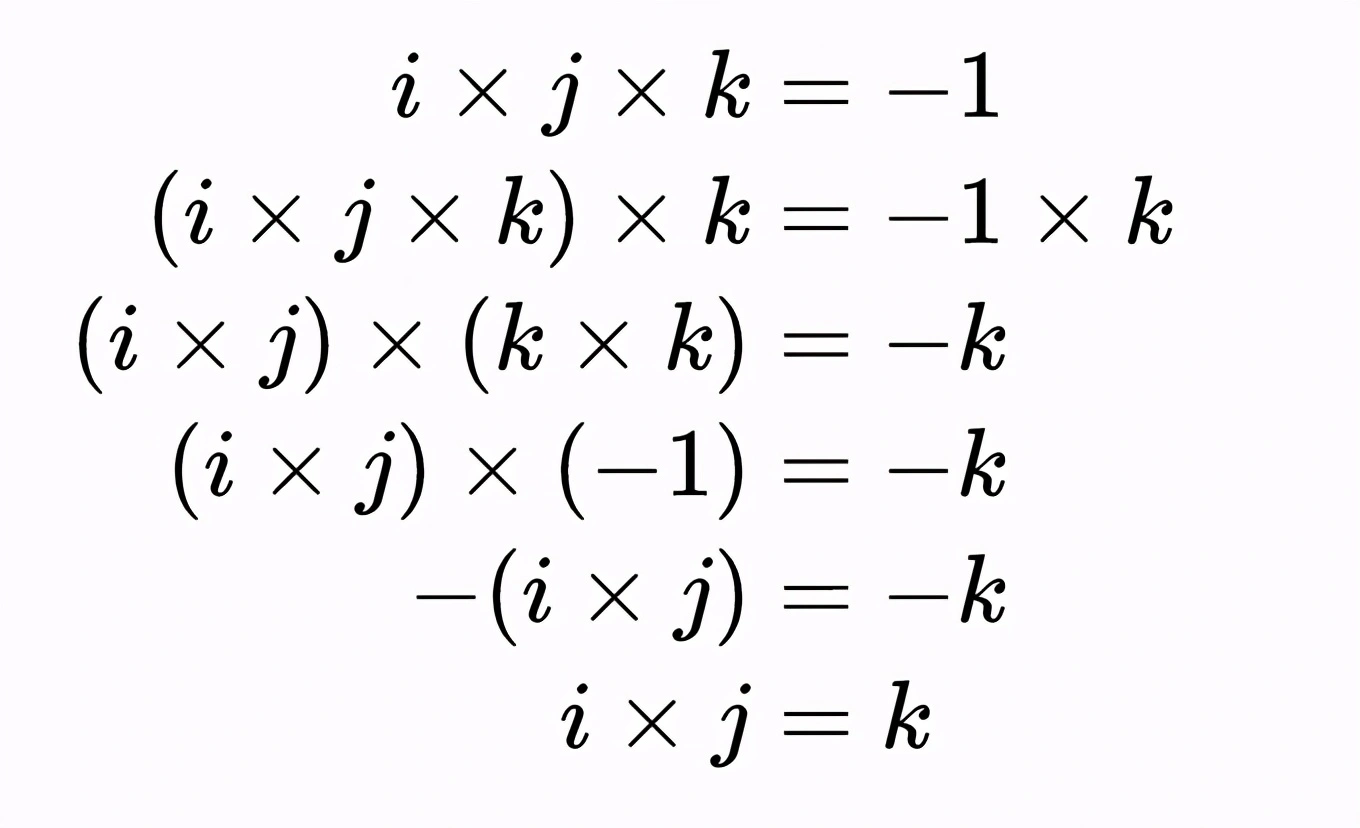
由汉密尔顿关系式可知,i × j = k。这里我们利用了k × k = -1以及其他性质,包括乘法的结合律。其他乘积可以用类似的方法推导出来,所以我们得到一个虚数单位的乘法表,就像这样:
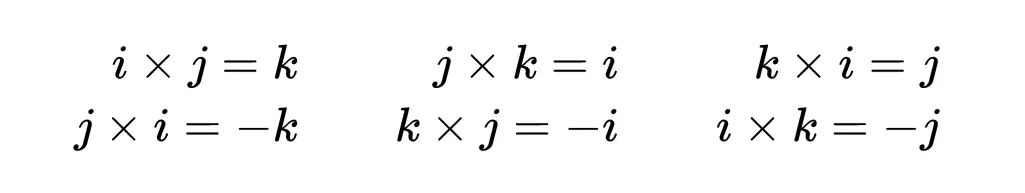
这些四元数乘法规则可以用下图表示:
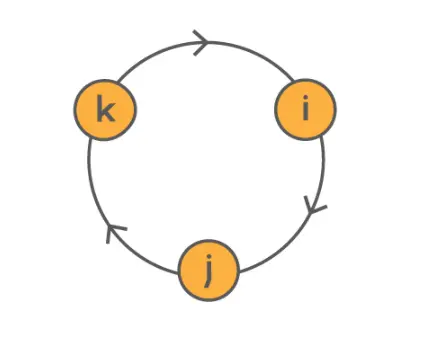
在这里,沿着箭头的方向绕圈会得到合适的乘积(如i × j = k),而沿着相反的方向移动会引入一个因子-1(如j × i = -k)。注意,这意味着,与实数和复数不同,四元数的乘法是不可交换的(不满足交换律)。
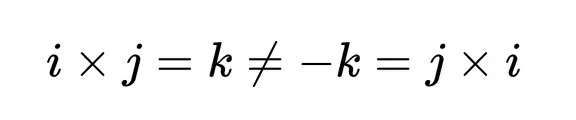
为了得到我们想要的四元数结构,我们必须放弃乘法的交换律。交换律是一种代数对称性,对称性在数学结构中一直是一个有用的性质。有了这些关系,我们就得到了一个可以加,减,乘,除的系统就像我们对复数做的一样。
四元数加减和复数一样。乘法还是要用到分配律。对于四元数的除法,我们仍然使用共轭的思想来求倒数,因为就像复数一样,任何四元数与其共轭的乘积都是实数。
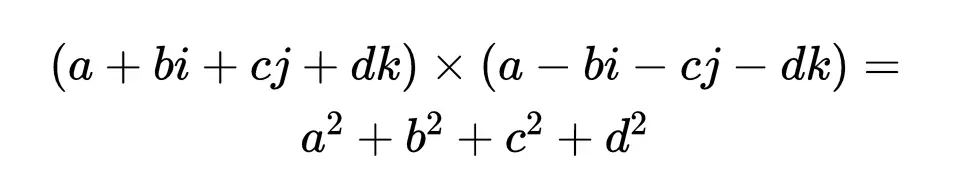
例如,如果我们想要除以四元数1 + i + j + k,我们利用(1 + i + j + k)(1 - i - j - k) = 4这一事实,可以求出1 + i + j + k的倒数,即:
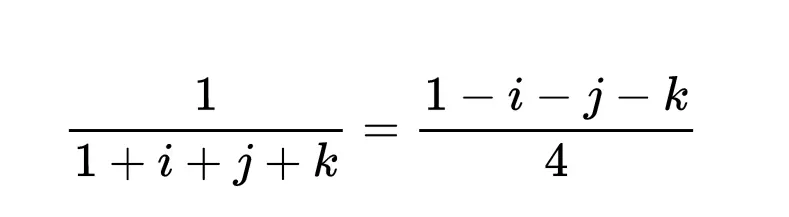
因此,四元数是复数的延伸,可以加、减、乘、除。和复数一样,四元数也非常有用,它们可以用来建模三维空间的旋转,这使得它们在渲染数字景观和球形视频,以及在我们的三维世界中定位宇宙飞船和手机等物体时非常有用。
这些超越实数的扩展仍然延续到八维八元,一个由汉密尔顿的同事发现的更奇怪的数字系统,它有七个虚单位。就像我们见过的其他数字系统一样,你可以对八元数加、减、乘、除。就像四元数一样,我们需要一些特殊的规则来控制如何乘所有的虚单位。这就是用“范诺平面”的图形表示出来的:
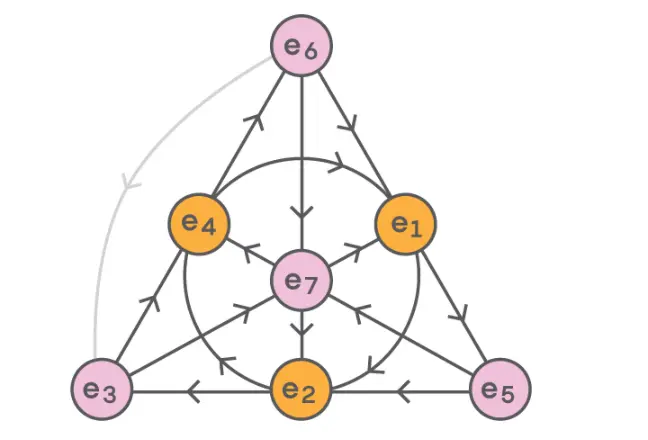
在四元数的表示中,沿着箭头方向相乘得到的是正乘积,而沿着反箭头方向相乘得到的是负乘积。
像四元数一样,八元数乘法是不可交换的。此外八元数也不满足结合律,当将三个八元数x、y、z相乘时,(x × y) × z = x × (y × z)并不一定是正确的。例如,用上面的图表,我们可以看到:
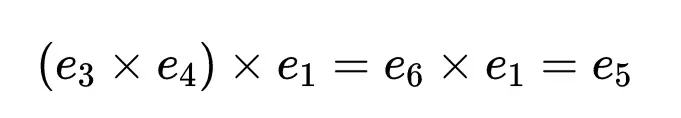
但:
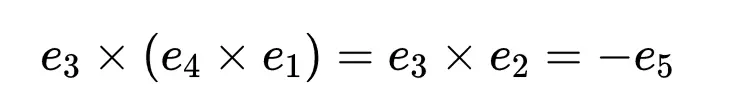
现在我们有了一个不满足交换律、不满足结合律的数字系统。它有什么用呢?一些物理学家认为八元数可能是描述强、弱和电磁力如何作用于夸克、轻子和它们的反粒子的关键。如果这是真的,这将有助于解决现代物理学中最大的谜团之一。
通过不断地扩展实数来创建更大的数字系统(复数、四元数、八元数),在这些系统中我们可以加、减、乘、除,每一次扩展都会有损失(四元数损失了交换律,八元数进一步损失了结合律)。在这个过程中,我们也可能与我们认为真实的东西失去联系。但我们得到的是思考世界的新方式。我们总能找到它的用处。
转载请超链接注明:头条资讯 » 现实边缘的数字,从四元数到八元数,将成为解决物理学困境的关键
免责声明
:非本网注明原创的信息,皆为程序自动获取互联网,目的在于传递更多信息,并不代表本网赞同其观点和对其真实性负责;如此页面有侵犯到您的权益,请给站长发送邮件,并提供相关证明(版权证明、身份证正反面、侵权链接),站长将在收到邮件24小时内删除。