我们人类生活在一个三维世界中。作为三维生物,没有什么比四维生物更可怕了。对我们来说,它们就像神,如果它们稍稍有点邪恶,就可以随心所欲地摧残和毁灭我们。
面对四维生物,人类没有任何物理装备和心理装备,所以任何更高维度的生物对我们来说都具有先天战术优势。
漫画集《奇幻故事之1963》(1963-Tales of the Uncanny,出版于1993年)在描述跨维度的战争时还算比较准确。在故事《它来自……高维空间!》(It Came from...Higher Space!)中,来自四维空间的生物攻击了一位三维空间的受害者。
漫画中的怪物由很多悬浮、分离的肢体构成。它在空中飞行,做出各种变形。
每当这只怪物出现时,半空中先出现一缕烟雾,然后烟雾像气球一样膨胀为三维体。作者将它描绘成一个肉做的甜甜圈,真是倒胃口。

想象一下三维生物攻击二维生物的情形,我们就可以解释为什么四维怪物的身体可以分离。
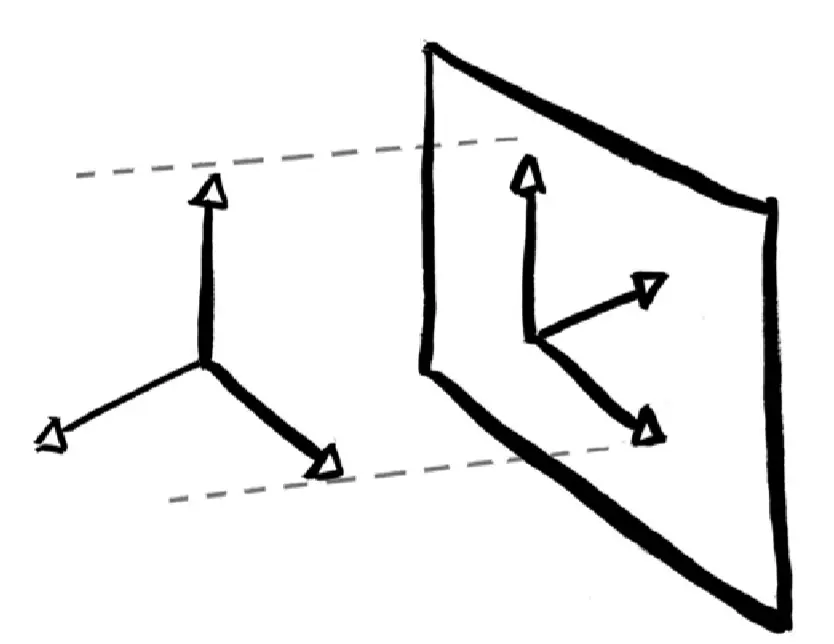
处于三维空间中意味着我们可以在3个不同的方向运动:左右、前后、上下,而二维生物只能在两个方向上移动:它们被限制在一个平面上。
让我们想象一个完全平的二维外星生物,姑且将其命名为平星人(hypoflatical),假设它们生活的宇宙是一个极其薄的平面。对我们来说,它们的宇宙就如同一张纸。我们可以从上方或下方悄悄地靠近它们的宇宙。
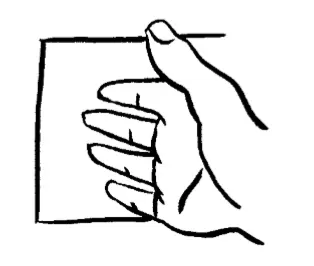
由于它们对第三维度没有概念,它们不知道我们在哪里。
三维空间为我们提供了完美的伪装。是时候向二维生物发起我们的恐怖袭击了,我们需要做的仅仅是从第三个方向进入它们的二维宇宙。
现在切换到平星人的视角。当我们的手指穿透它们的二维世界,它们会看到几个悬浮的圆盘渐渐变大、接近。
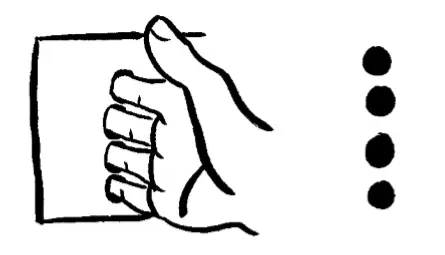
进而当手掌进入二维世界,这些圆盘便会合并起来。平星人只能看到我们手的二维截面,它就像在空中飞的肉饼。

(二维平面旁边的手不会被发现。只有当手逐渐穿过二维世界,它与二维世界相交的部分才会被平星人看到)
平星人躲起来也没用:作为三维生物,我们可以像看平面设计图一样看到整个二维世界——阿兰·摩尔故事中的四维生物也是这样看待我们三维世界的。
因此,平星人没法躲到什么东西后面,也没法把自己锁进安全的角落。对我们来说,进出封闭的二维世界如同进出二维正方形那样简单。

我们还可以清楚地看到二维生物的内部:它们体内的所有器官都会展现在我们面前,任我们摆布。
这正是四维生物对三维生物造成的威胁:它们潜伏在三维宇宙旁边,静静地观察我们的一举一动和我们身体的所有部件;它们可以轻而易举进入我们的身体,并从内部将我们杀死。

这些怪物是我们的噩梦,不过幸好,没有证据表明四维生物是存在的,但对四维空间多些了解并没有什么坏处,以防万一嘛。
假如我们是仁慈的三维生物,本着跨维度交流的善意,欲向平星人展示我们的三维世界—向它们讲解它们之外的世界是什么样的,例如,向它们展示三维立方体。
如果我们将立方体移入平星人的二维世界,它们只会看到各种不同的截面。最无趣的方式是先推入正方体的一个面,这样只能让它们看到一个正方形突然出现,然后又突然消失。
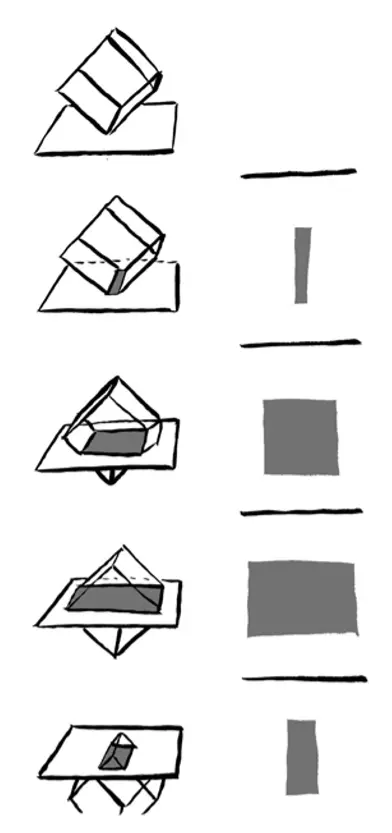
(当三维立方体从一条边开始穿越二维平面时,平星人看到的景象)
稍微有趣的方式是先推入一条棱,这样它们会看到一个长方形从无到有,慢慢变大,然后再慢慢缩小到无。
不过最有趣的方式是先推入一个顶点,平星人会看到一个三角形从无到有,慢慢变大,接着三 角形会发生各种形状的变化,最终又收缩到无。对于限制在平面上的平星人来说,这是再新奇不过的事了。
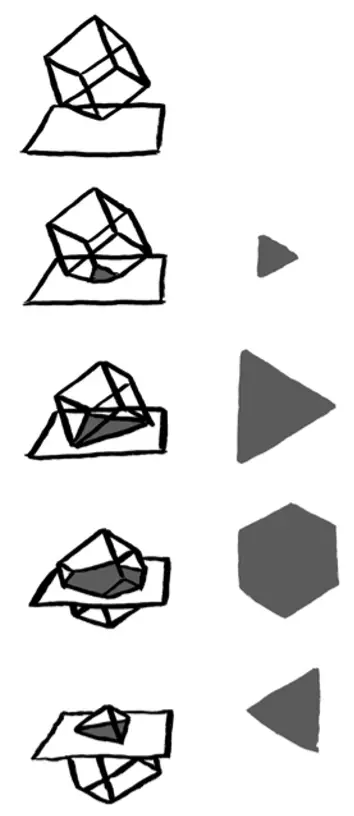
(当三维立方体从一个顶点开始穿越二维平面时,平星人看到的景象)
而且我们还会发现,这种进入方式和我们提到过的一个数学问题有所关联:
如果我们能够跟踪记录变化截面覆盖过的所有区域,它会是一个完美的正六边形;不仅如此,它恰好是我们在解决鲁珀特王子的立方体穿过难题时遇到的立方体截面图。
现在,让我们来仔细思考四维超立方体(hypercube)穿越我们的三维世界会发生什么事情。
假设一个友善的四维生物也本着跨维度交流的善意,向我们展示四维超立方体。当超立方体穿越我们的三维世界时,我们会看到它的一系列三维截面。



滑动看情绪逐渐暴躁的四维图形
最无趣的方式仍然是从面开始穿越,我们只能看到一个普通的三维立方体突然出现,然后又突然消失。
如果超立方体从棱开始穿越,事情就变得有趣得多了。我们会看到一个三棱柱从无到有,慢慢变大,然后变形为六棱柱,接着再变成与之前方向相反的三棱柱,最终慢慢消失。
最有趣的仍然是超立方体从一个顶点开始穿越我们的三维世界。
此时,一个四面体凭空出现并均匀地变大,然后变形成一个由六边形和三角形组成的奇怪图形,有那么一瞬间变成了正八面体,然后又倒着变回了之前的那些图形(只不过方向相反),直至缩小消失。
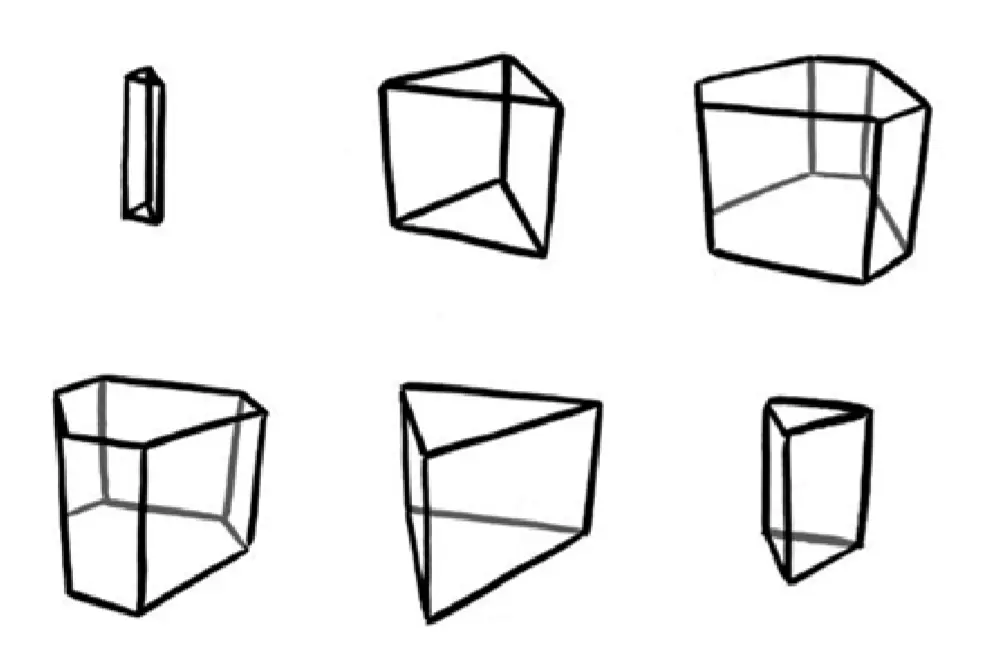
(当四维立方体从棱开始穿过我们的世界时,三维截面的变化情况。其覆盖的所有空间会形成一个六棱柱)
我觉得这才能算作高大上的形象嘛。
我们再次探讨一下穿越过程中出现的各种形状。如果你把四维立方体分成完全相同的两半,去寻找最大的三维截面,你会得到一个正八面体的截面,也就是三维立方体的对偶图形。
在穿越三维空间的过程中,四维立方体覆盖的所有空间会形成一个菱形十二面体(rhombic dodecahedron)。
然而,所有这些都无法告诉我们四维立方体的全貌。多说无益,让我们一起动手做出这些形状的模型吧。
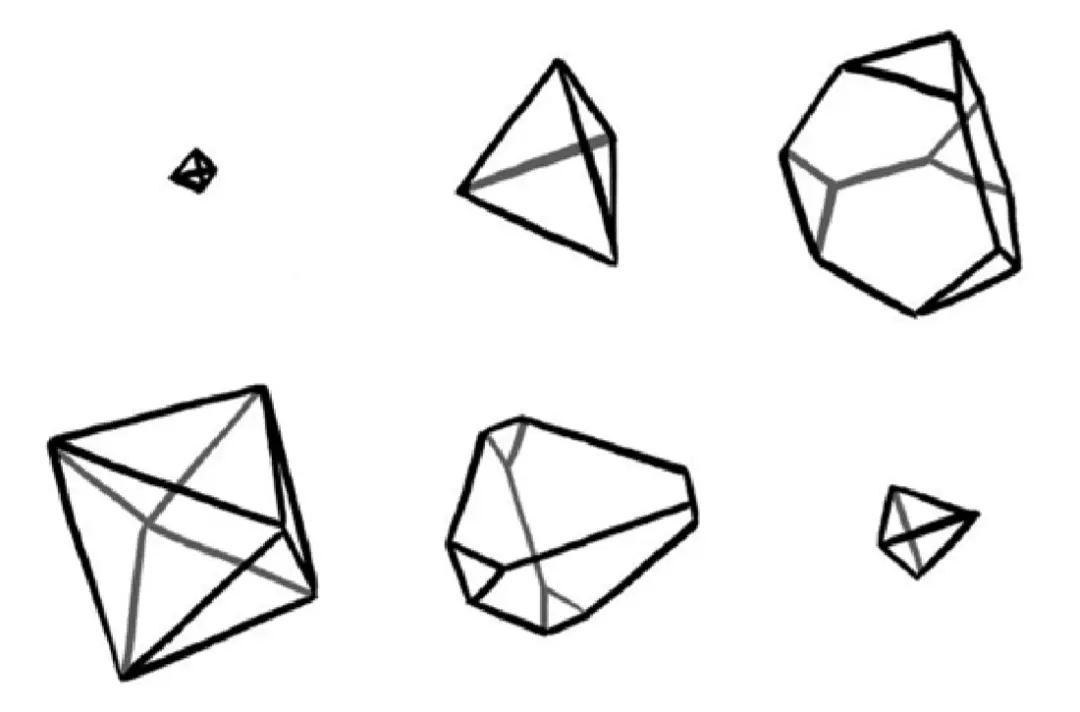
(当四维立方体从顶点开始穿越我们的世界时,三维截面的变化情况。有趣的是:在穿越过程中,四维立方体覆盖的所有空间会形成一个菱形十二面体)
现在我们可以用吸管来构建一个四维立方体。和制作空间填充维埃尔——费伦模型时一样,我们仍使用彩色吸管,但在这里,不同的颜色代表不同的方向。
让我们先从低维开始,然后不断增加维数。制作一个一维图形非常容易:一根吸管就是一个一维图形。我们用红色代表唯一的方向。

(一维的线)
制作二维图形也没有增加多少难度。和先前一样,我们用弯曲的吸管刷来连接红色吸管(代表水平方向)和蓝色吸管(代表垂直方向)的末端。
这时我们可以在两个方向自由移动。其实对于平星人来说,这也是轻而易举的把戏。
我们可以这样理解二维正方形:将一维的边复制成两条,然后将它们用另外一方向的两条边连接起来。

(二维的正方形)
类似的,三维立方体可以理解为将二维正方形复制了一次,然后将两个正方形的顶点通过第三个方向上的新边连接起来。
因此,你只需要按照刚才的配色再做一个正方形,然后用另一种颜色的吸管(比如绿色)将两个正方形的顶点对应连接起来,便能得到三维立方体模型了。
出于习惯,你可能会将模型做成直立的。然而,为了向平星人展示立方体,我们可以将立方体压扁在一个平面上。
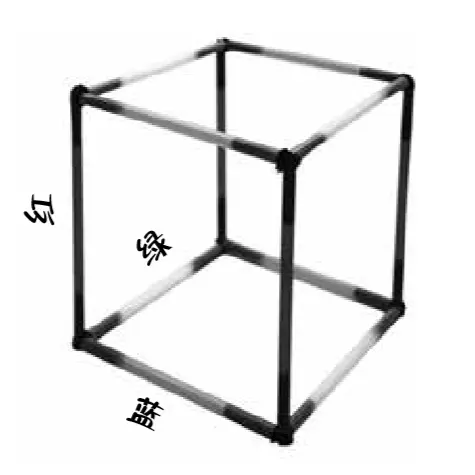
(三维的立方体)
为了使立方体变成四维的,我们要复制一个立方体,然后将这两个立方体的顶点用另一种颜色的吸管(比如黄色)连接起来,这种颜色就代表第四个方向。这个模型和我们向平星人展示的立方体类似。
在我们展示三维立方体时,第二个正方形本该被擡离二维平面变成三维,但是我们把它压到了第一个正方形的旁边。
在这里,第二立方体本该被擡离我们的三维曲面,进入第四维,但是我们让它落在第一个立方体的旁边。
这个模型是一个完整的四维立方体,只不过为了适应我们可怜的三维世界,被压平了。
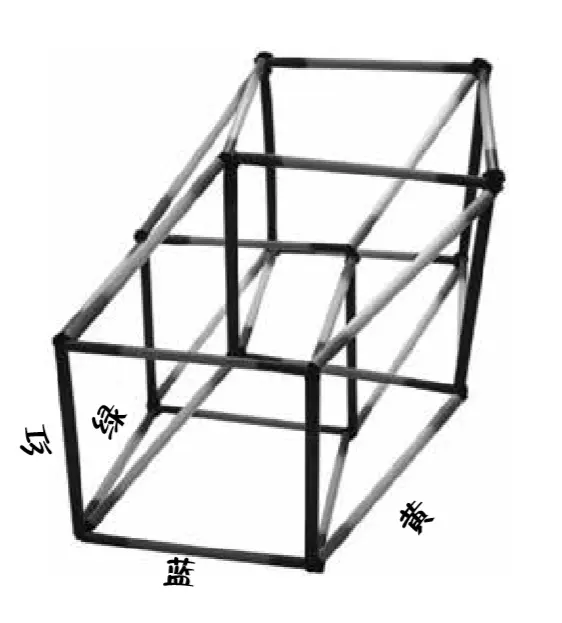
(四维超立方体)
平面版的三维立方体形状和立方体的投影相同。如果我们利用光将三维立方体投影到一个平面上,就能看到它的二维投影,而这正是平星人看到的三维世界。
仁慈的四维生物也可以用同样的方式将四维图形进行投影,向我们展示它的三维投影:你制作的四维吸管立方体模型便是四维立方体的一个三维投影。
不过我们还可以通过另一种方式得到投影:引入透视。如果将三维立方体的第二个正方形缩小一点,使其悬浮在第一个正方形内部,便可得到立方体的平面投影,边与边之间不会相交。

同样,我们也可以将四维立方体的第二个三维立方体做小一些,使其悬浮在第一个立方体内部,从而获得四维立方体在三维空间的投影,面与面之间不会相交。
是不是有似曾相识的感觉?你在这之前确实见过类似的四维立方体——立方体状肥皂泡。当时你已经在不经意间用肥皂膜做出了一个四维立方体的三维投影。
除了通过透视来研究高维图形,我们还可以通过研究旋转立方体的投影。
为了获得旋转三维立方体的二维投影,将其中一组相对的面染上颜色,将其他4个相邻的面留白,这样可以帮助我们跟踪立方体的旋转。

(加入些许透视,便可避免图形的自相交)
我们还可以利用这个旋转的投影向平星人展示三维立方体。虽然立方体在平星人二维宇宙旁边的三维空间旋转,但平星人能够通过正方形的投影做出判断。
影子越来越大,表明正方体正在向它们靠近;反之,投影越来越小,表明正方体正在远离它们。
不幸的是,在它们看来,两个正方形不断穿过对方。所有的解释都无法让平星人看到这两个 正方形在更高的维度中没有相交,而是处于前后不同的位置。
(旋转三维立方体的二维投影和旋转四维立方体的三维投影,上下两张图同时转完半圈)
同样,我们也可以将旋转的四维立方体投影到三维世界。我们仍然将其中一组相对的立方体染色,起连接作用的其他立方体则是透明的。
当这个四维立方体在我们的三维宇宙之外旋转时,每个立方体离我们更近时都会变大,离我们更远时都会变小。
遗憾的是,和平星人一样,在我们看来,这两个方体不断相交,但实际上,这两个立方体在四维空间中属于前后的关系,只是我们无法看到这一点。
当三维立方体的一个二维面刚好与影子所在的二维平面垂直时,它的投影会短暂地消失。

(一个没有复原的四维魔方)
同样,当四维立方体的一个三维立方体恰好与我们的三维宇宙垂直时,它也会从我们的视线中短暂消失。
不可思议的第四维度!
如果你想自己试着转一转四维立方体,我建议你尝试研究四维魔方(Rubik’s Cube)。
三维魔方需要将颜色相同的二维色块移动到三维立方体的同一个二维面上,但四维魔方有些不同,你需要将颜色相同的三维色块移动到四维立方体的同一个三维面上。
你无法直接变换四维立方体,但是你可以通过拖拽四维魔方的三维投影来间接地进行变换,这种魔方可以在网上找到。
玩的时候你脑子会特别晕,因为三维投影可以在我们熟悉的三个方向上运动,但四维立方体还能在第四个正交(orthogonal,即交角为直角)的方向上旋转(网站上是通过按住shift键实现的)。
不过有点糟糕的是,因为你只能在电脑屏幕上看到四维魔方的三维投影,所以实际上你处理的是四维立方体的三维投影的二维投影,我只能祝你好运了。
来源:遇见数学
编辑:荔枝
转载请超链接注明:头条资讯 » 高维生物的快乐你真的想象不到吗
免责声明
:非本网注明原创的信息,皆为程序自动获取互联网,目的在于传递更多信息,并不代表本网赞同其观点和对其真实性负责;如此页面有侵犯到您的权益,请给站长发送邮件,并提供相关证明(版权证明、身份证正反面、侵权链接),站长将在收到邮件24小时内删除。