
在爱因斯坦广义相对论(他的引力理论)的原始公式中,基本场是度规张量g,这个理论在时空中是协变的。协方差由“物理定律在任意座标变换下的形式的不变性”组成。这个想法是,由于座标只是人造的标签,物理定律不应该取决于它们选择的方式。
在广义相对论中,这种运动(一个系统动力学的一个属性,从这个属性可以导出它的运动方程)被称为爱因斯坦-希尔伯特运动:
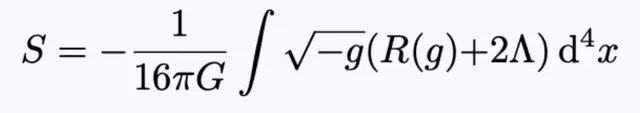
方程1:爱因斯坦-希尔伯特作用
其中g = det(g),R(g)是标量曲率,这是一个测量曲线流形中小球的体积与欧几里得空间中小球体积的差别的方法,G是牛顿常数,Λ是宇宙常数或真空能。注意,如果时空是有界的,S应该包含一个边界积分。为了简单起见,让我们假设物质不存在。

爱因斯坦和希尔伯特。
要求这个作用力相对于度规的变化为零,我们得到爱因斯坦的无源场方程:
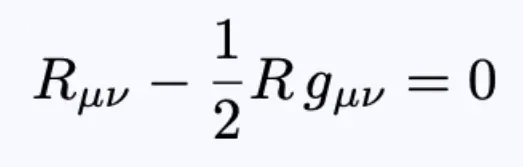
方程2:无物质条件下的爱因斯坦场方程。
R是里奇曲率张量。
用粒子力学作类比可能有助于阐明这些观点。在拉格朗日力学中,我们给出一个拉格朗日L,我们构造一个作用泛函S,通过对S求极值得到运动方程:
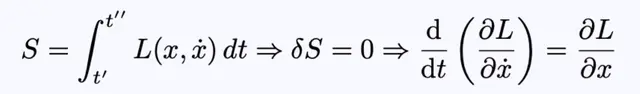
方程3:给定一个拉格朗日L,对作用函数S求极值,得到运动方程。
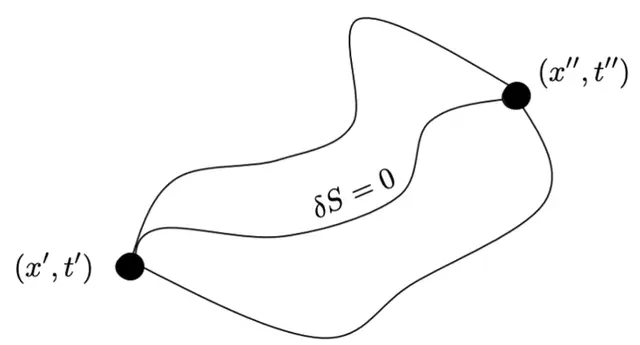
图1:质点选择使运动达到极值的路径。
本文的目的
这篇文章的目的是说明时间编码在空间的几何形状中。这个程序遵循了拜尔莱因、夏普和惠勒在1962年发表的论文(我们称这篇论文为BSW)。用米斯纳、索恩和惠勒的著名著作《万有引力》中的话来说,“三维几何是关于时间的信息载体”。
发生这种情况的原因如下。将方程3中的拉格朗日方法推广到广义相对论,我们将得到:
具有内在几何结构的初始三维表面(下面方程4的第一项)。
第二个三维曲面也具有相关的内在几何(方程4的第二项)。
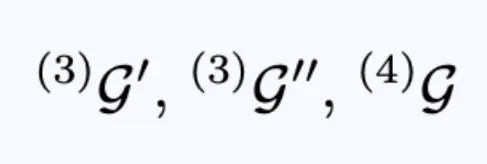
方程4:上述两个三维曲面的本征几何和四维时空的几何。
目标是找到一个四维几何(方程4的第三项),满足爱因斯坦方程(方程2),并简化为三面σ和σ'上的三维几何。为此,他们发展了一种变分原理(所谓的“压缩薄夹层变分原理”),它只依赖于两个三表面的内在性质。根据他们的程序,我们:
找出两个三维表面之间的时间间隔。
找出这些表面在时空中的位置。
在这样的四维时空中,每个三维几何都仅基于两个固有几何而被很好地指定。
在进一步讨论之前,对所谓的广义相对论ADM形式主义有一个概念是至关重要的。这将是下一节的主题。
ADM形式主义的鸟瞰图
在ADM形式主义中,广义相对论被表述为一个动力学理论,以其作者Ricard Arnowitt, Stanley Deser和Charles Misner命名。

图2:Richard Arnowitt, Stanley Deser和Charles Misner。
广义相对论的动力学被称为几何学动力学。正如我们将在本节中看到的,广义相对论中的“变化的东西”是嵌入四维时空中的三维表面内的距离(而不是四维时空距离)。
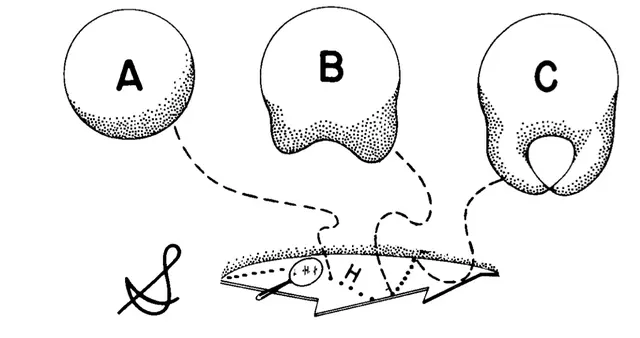
图3:几何动力学的超空间。
在广义相对论的这个动态版本中,位形空间被称为超空间。
ADM结构如下图所示:
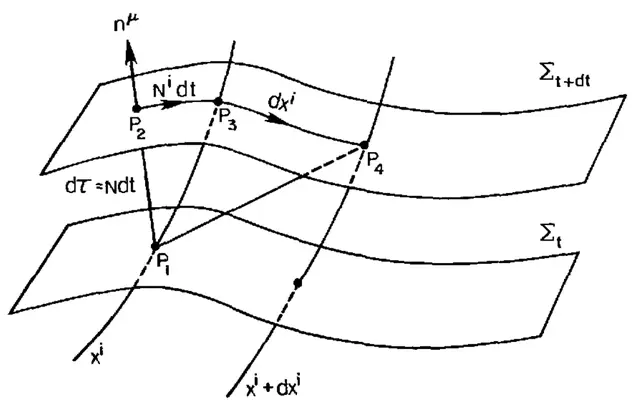
图4:ADM结构。嵌入四维时空中的两个三维表面(三几何图形)。
位移矢量N,如图所示,是表面随时间变化的变形的度量。两表面之间的适当距离是dτ = N₀ dt,其中N₀ 是失效函数。
使用图2,我们可以用移位和延时来重写ds²:
方程5:P₁与P₄之间的距离。
其中第二个等式后的张量g是三个曲面的度规。嵌入在四维时空中的三维超曲面的外在曲率有以下形式:
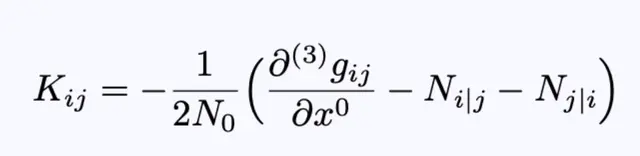
方程6:超曲面的外在曲率。
其中符号“|”表示曲面内部的内在空间度量的协变微分。
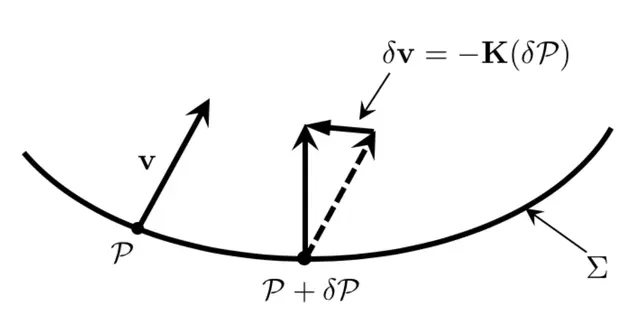
图5:外部曲率。
里奇标量R可以用外在曲率K表示,它的轨迹是K。表示本征曲率:
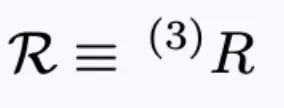
方程7:重命名本征曲率。
里奇标量可以写成:
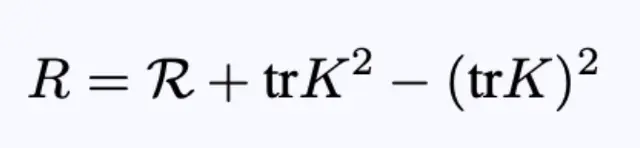
方程8:用外在曲率、它的轨迹和三个曲率表示的里奇标量。
则拉格朗日密度为:
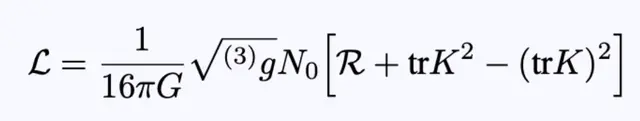
方程9:引力拉格朗日密度以三曲率、外在曲率及其轨迹表示。
拉格朗日密度不依赖于位移和位移的时间导数。
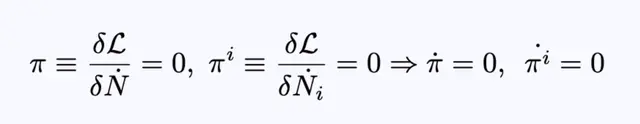
方程10。
偏差和位移在任何时候都是零,因此不是动态变量,因此,我们有:
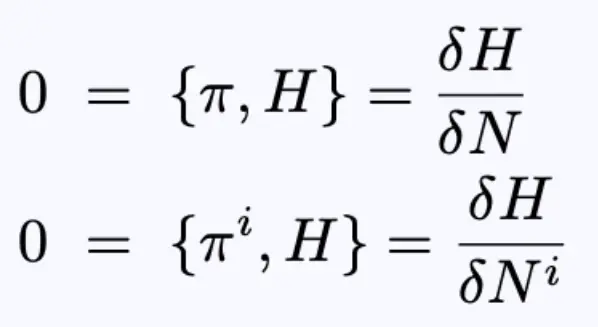
方程11:哈密顿函数H的条件。
由H表达式可知:
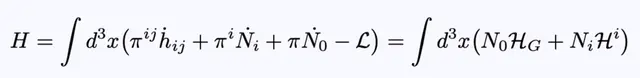
方程12:使用ADM变量的哈密顿量。
我们定义:
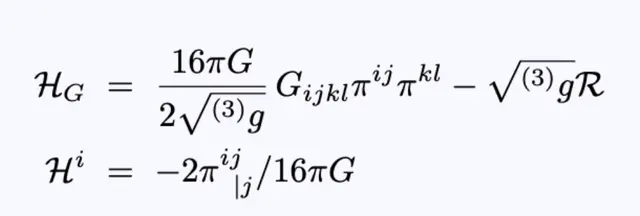
方程13:方程12中第二个等式后对象的定义。
第一个方程中的张量G由:
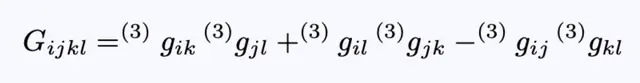
被称为惠勒-德维特度规。
最后,利用公式11,我们得到了一个有约束的哈密顿动力学系统的方程,它是对爱因斯坦场方程的重新表述,它描述了三个度量的演化:
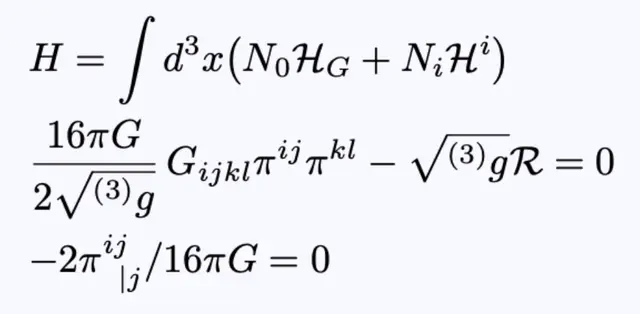
方程14:描述三度量演化的哈密顿动力学系统的约束方程。
20世纪最重要的物理学家之一保罗·狄拉克,以及美国理论物理学家约翰·惠勒都被哈密顿公式的简单性所折服,他质疑时空的状态。
狄拉克宣称:
这个结果让我开始怀疑四维物理条件到底有多基本。几十年前,人们似乎很肯定必须把整个物理学用四维形式表达出来。但现在看来,四维对称似乎并不是那么重要,因为人们一旦脱离了自然,对自然的描述有时就变得简单化了。
惠勒写道:
这里的动态物体不是时空,而是空间。空间的几何形态随时间而变化。但变化的是空间,三维空间。在粒子动力学中,动力学的对象不是x和t,而是只有x…答案很简单。爱因斯坦的几何学动力学处理的是几何学的动力学,是三维几何,而不是四维几何。

图6:保罗·狄拉克和约翰·惠勒。
利用几何动力学和方程9得到的作用,可以通过以下公式确定弯曲空空间演化的三几何时间演化:
初始表面的几何形状
初始曲面K的外曲率,描述了它在时空中的嵌入,将用爱因斯坦方程构造(见图3)。
但是,h和K不能单独指定。它们必须服从Foures和Lichnerowicz的初值方程。
拜尔林,夏普和惠勒程序
现在我将描述BSW中的步骤。
步骤1
首先,选择两个非常相似(几乎完全相同)的三维指标:
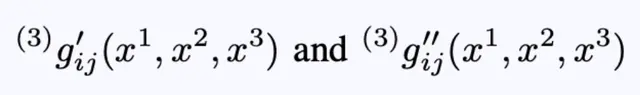
方程15:两个几乎相同的三维度量。
两个表面之间的时间间隔是有限的,为了方便起见,取δx⁰=1。
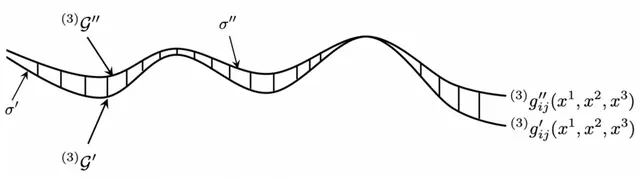
图7:两个三维表面的说明。
步骤2
下一步是用尚未确定的四几何图形填充表面之间的区域。用座标表示两点之间的距离:
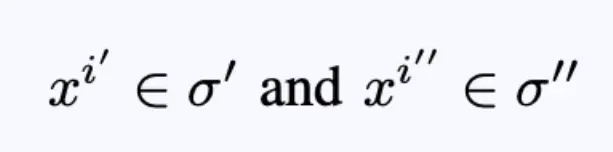
方程16:两个点的座标,每个面上各一个点。
是由:
方程17:式(16)中两点间的线元
这里η₀是失效函。
步骤3
四几何图形是以下BSW作用的极值,并以两个三面的几何图形为边界条件,满足爱因斯坦场方程。
作用积分为:
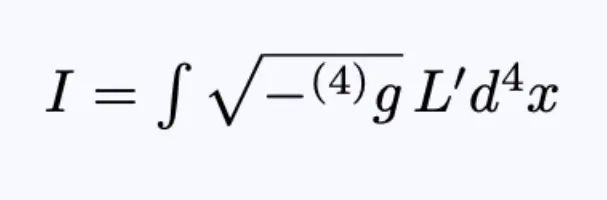
方程18:作用积分。
在ADM语言中,它变成:
方程19:用ADM形式表示的作用积分。
π是几何动力场动量共轭到几何动力场座标³g,定义为:
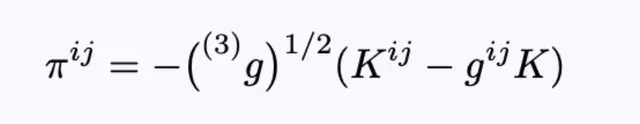
方程20:ADM场动量π。
竖条表示三面内的协变导数。
步骤4
现在假设这三个几何图形几乎是相同的。然后,我们有:

方程21:三个几何形状几乎相同时的体积元。
用以下三度规在垂直于曲面方向上的非归一化时间导数来代替外在曲率:
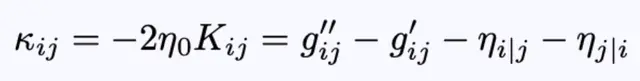
方程22:三度规在垂直于曲面方向上的非归一化时间导数。
使用方程21,作用变成:
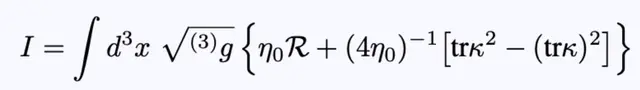
方程23:三个几何图形几乎相同时的作用。
步骤5
现在求关于η₀的极值,得到:
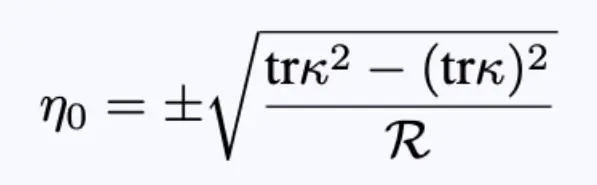
方程24:两个三面之间的固有时分离。
这是两个三面之间的固有时间间隔。
步骤6
注意,η依赖于k, k依赖于位移向量ηᵢ(x¹,x²,x³),为了得到ηᵢ(x¹,x²,x³),把方程22带入到方程23,结果是:
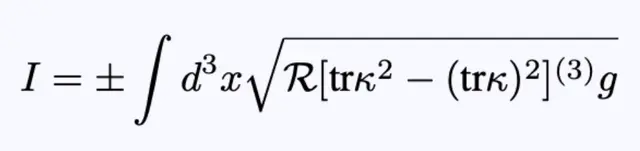
方程25:只改变位移矢量分量的运动。
η₀被舍弃。然后改变动作I只与分量有关。
步骤7
下一步是求解步骤6中ηᵢ的方程,并将其代入方程22和方程24。因此,根据两个三面的固有几何,找到时间间隔η₀。
步骤8
外部曲率K由式22得到。可以证明,使用爱因斯坦场方程与初始的三度规和外在曲率K一起确定表面嵌入的时空的度规。因此,BSW展示了如何找到两个表面之间的时间间隔,以及它们在给定的两个三维几何图形中的时空位置。
转载请超链接注明:头条资讯 » 为什么时间被编码在空间几何中?通过理论计算证明
免责声明
:非本网注明原创的信息,皆为程序自动获取互联网,目的在于传递更多信息,并不代表本网赞同其观点和对其真实性负责;如此页面有侵犯到您的权益,请给站长发送邮件,并提供相关证明(版权证明、身份证正反面、侵权链接),站长将在收到邮件24小时内删除。