當你第一次遇到“虛數”時,你是否會想,我什麼時候才能用它?虛數以及由它組成的複數是非常有用的。它對物理學、工程學、數論和幾何都有深遠的影響。它們是進入奇異數字系統世界的第一步,其中一些數字系統被提出作為我們物理世界的模型。讓我們來看看它是如何紮根於我們已知的數字系統,但與此同時,卻不像我們想象的那樣。
實數是我們最熟悉的數學對象,它們都是可以用十進製表示的數字,如5、8.2、-13.712、0、10.33333…。我們可以對實數進行加、減、乘、除運算,在日常生活中,我們都用實數來回答問題。但是實數並不足以解決所有的數學問題。
在16世紀,方程求解大師吉羅拉莫·卡達諾試圖解多項式方程。他毫不費力地解出 x^2-8x+12=0這樣的方程,因為很容易找到兩個和為8,積為12的數(2和6)。這意味著可以將這個多項式表示為兩個因子的乘積(x-2)(x-6)。
但對於x^2-3x+10=0這樣的方程就不那麼容易了。找到兩個和為3積為10的數似乎是不可能的。然而,卡達諾發現,如果給-1的平方根賦值,就能找到這樣的數。這是一個令人不安的發現。當平方一個實數時,結果永遠不會是負數。這意味著沒有實數的平方可以等於-1。卡達諾用-1的平方根來解他的實數方程,但-1的平方根不是實數。
卡達諾非常謹慎地對待這些非實數,他驚訝地發現,它們遵循著許多與實數相同的規則。卡達諾的發現導致了複數的發展,這是實數的一個強大而有效的擴展。
複數由實部和虛部組成。它們的形式是a + bi,其中a和b都是實數,i被稱為虛單位。乍一看,它們似乎很奇怪,但我們很快就會發現複數的加減乘除運算與實數的運算是一樣的。
要加減複數,只需將實部和虛部合併,就像這樣:
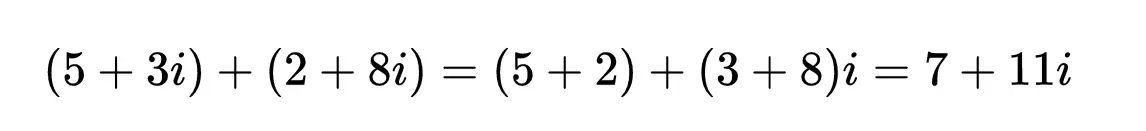
複數的乘法與實數的分配律是一樣的。例如,當2和5 + i相乘時:
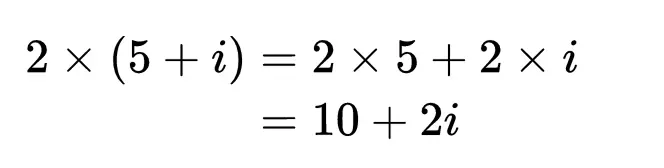
要將2 + 3i和5 + i相乘,只需應用兩次分配律:
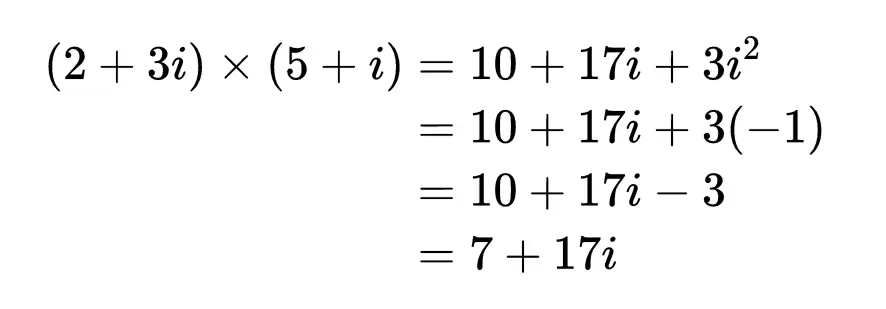
兩個複數相乘仍然得到複數,這說明覆數就有“閉包”性質。複數的乘法是符合交換律的。我們可以把複數相乘,但是怎麼做除法呢?關鍵在於理解除法和乘法之間的關係。
在學校,老師可能講過,沒有除法,只有倒數的乘法。一個非零實數a的倒數是1/a。但當你開始考慮像1/i這樣的數字時,它的含義可能不是很清楚,但i的倒數是與i相乘得到1的數。你可能會有點驚訝,這個數字是-i !
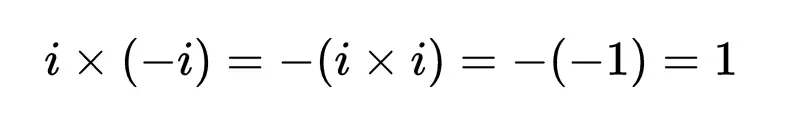
使用i×i= –1這一事實,以及實數和複數的一些重要性質,我們看到i × (-i) = 1,那麼-i就是i的倒數。這意味著如果我們想用i除一個數,我們可以用-i來代替作乘法。
對於其他複數,計算可能會有點困難,但是倒數的思想仍然有效。例如,要計算(1+2i)/(3+4i),我們需要找到3+ 4i的倒數,為此,我們將使用複數的“共軛”技巧,也就是改變其虛部的符號時得到的數。
當複數3 + 4i乘以它的共軛3 - 4i會發生什麼?(3+4i)×(3−4i)
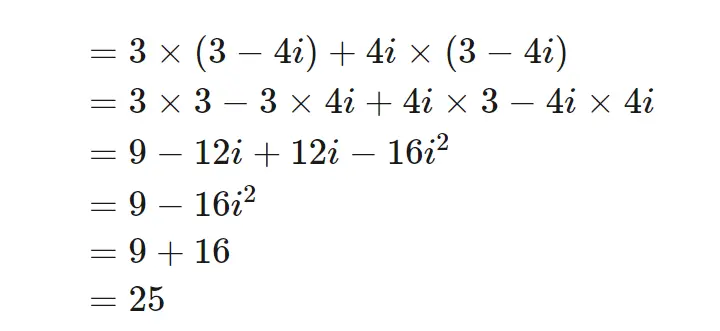
複數與其共軛的乘積是實數。共軛的這個性質幫助我們計算任何複數的倒數。由於(3 + 4i) × (3 - 4i) = 25,方程兩邊同時除以25,做一些代數運算:
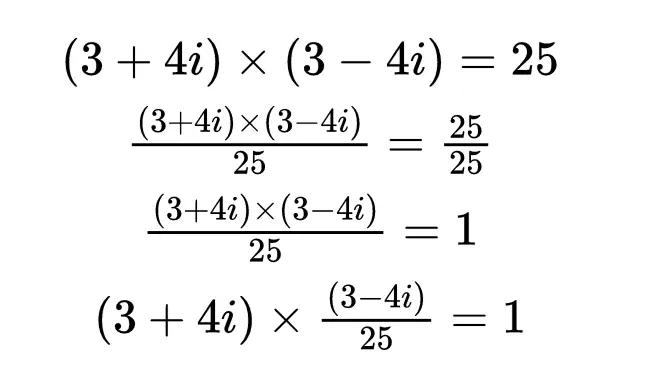
請點擊輸入圖片描述
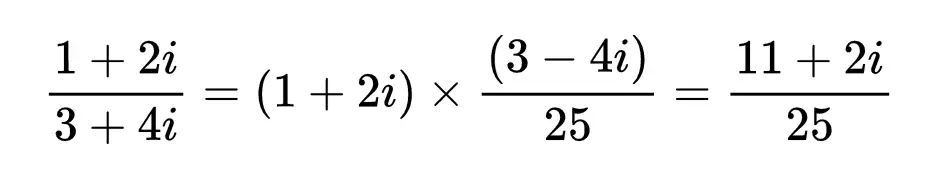
引入了這一新的非實數i(虛單位),開啟了一個全新的數學世界。這是一個奇怪的世界,平方可以是負的,但它的結構與我們所熟悉的實數非常相似。而這種對實數的擴展僅僅是個開始。
1843年,威廉·羅文·漢密爾頓想象了一個世界,其中有許多不同的“虛單位”,並在此過程中發現了四元數。四元數的結構與複數相似,但有額外的-1的平方根,漢密爾頓稱之為j和k。每個四元數的形式為a + bi + cj +dk,其中a, b, c和d是實數, i^2=j^2=k^2=-1。你可能認為任何人都可以發明一個新的數字系統,但重要的是要問它是否具有我們想要的結構和屬性。例如,該系統在乘法下是封閉的嗎?
為了確保四元數具有這些屬性(封閉性,四元數相乘仍然是四元數),漢密爾頓必須弄清楚如何處理i × j。所有四元數需要看起來像a + bi + cj +dk,但i × j並不像。當我們第一次將兩個複數相乘時,我們遇到了類似的問題,結果中有一個i × i項,但我們可以利用 i^2=-1這一事實來將這個數字轉換成正確的複數形式(從而保證了複數在乘法下封閉)。但是如果i^2=−1i × j呢?
漢密爾頓自己也在努力思考這個問題,當靈感終於到來的時候,他把自己的見解刻在了橋的石頭上:
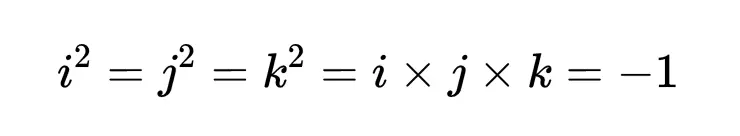
來自世界各地的人們仍然會訪問都柏林的布魯姆橋來分享這一數學發現的時刻。
漢密爾頓在虛單位i、j和k之間的著名關係允許我們對四元數進行乘法和除法,並得到我們最期望的結果。從i × j × k = -1開始,我們在方程的兩邊乘以k並化簡。
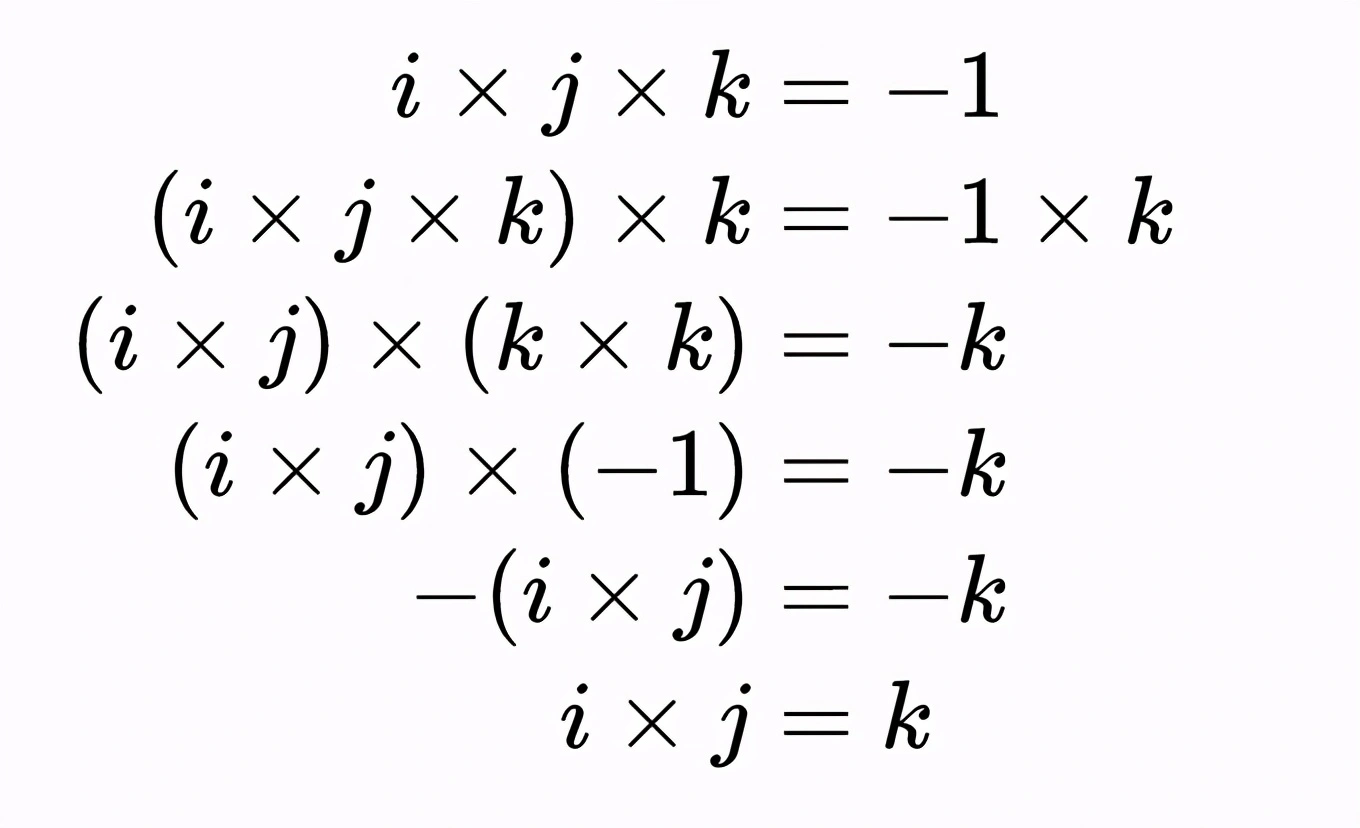
由漢密爾頓關係式可知,i × j = k。這裡我們利用了k × k = -1以及其他性質,包括乘法的結合律。其他乘積可以用類似的方法推導出來,所以我們得到一個虛數單位的乘法表,就像這樣:
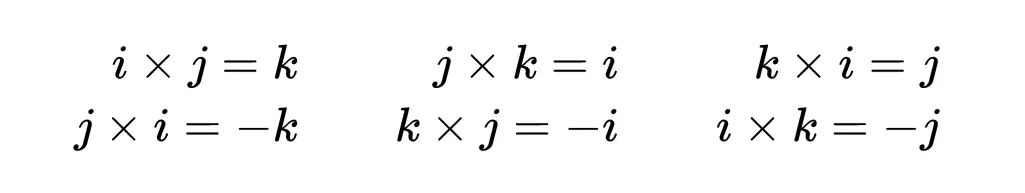
這些四元數乘法規則可以用下圖表示:
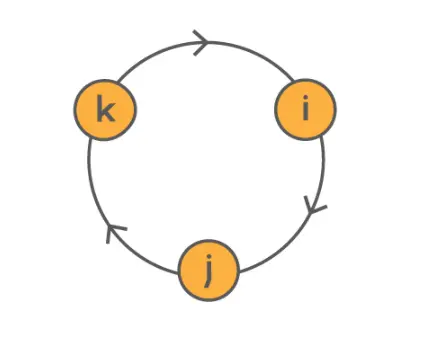
在這裡,沿著箭頭的方向繞圈會得到合適的乘積(如i × j = k),而沿著相反的方向移動會引入一個因子-1(如j × i = -k)。注意,這意味著,與實數和複數不同,四元數的乘法是不可交換的(不滿足交換律)。
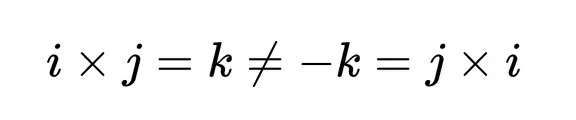
為了得到我們想要的四元數結構,我們必須放棄乘法的交換律。交換律是一種代數對稱性,對稱性在數學結構中一直是一個有用的性質。有了這些關係,我們就得到了一個可以加,減,乘,除的系統就像我們對複數做的一樣。
四元數加減和複數一樣。乘法還是要用到分配律。對於四元數的除法,我們仍然使用共軛的思想來求倒數,因為就像複數一樣,任何四元數與其共軛的乘積都是實數。
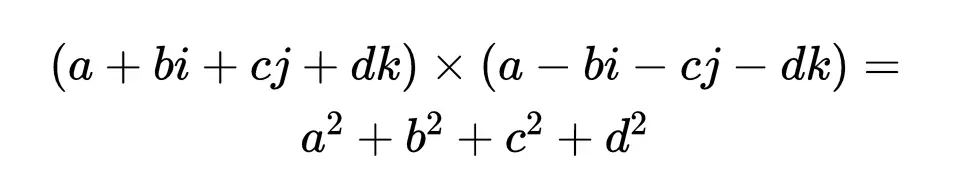
例如,如果我們想要除以四元數1 + i + j + k,我們利用(1 + i + j + k)(1 - i - j - k) = 4這一事實,可以求出1 + i + j + k的倒數,即:
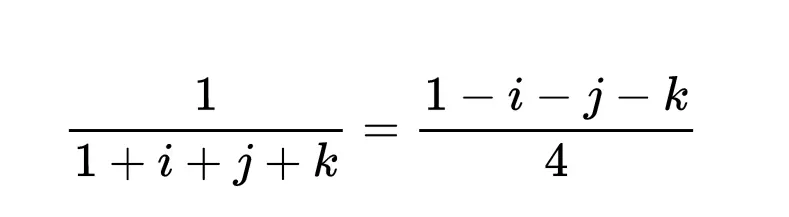
因此,四元數是複數的延伸,可以加、減、乘、除。和複數一樣,四元數也非常有用,它們可以用來建模三維空間的旋轉,這使得它們在渲染數字景觀和球形視頻,以及在我們的三維世界中定位宇宙飛船和手機等物體時非常有用。
這些超越實數的擴展仍然延續到八維八元,一個由漢密爾頓的同事發現的更奇怪的數字系統,它有七個虛單位。就像我們見過的其他數字系統一樣,你可以對八元數加、減、乘、除。就像四元數一樣,我們需要一些特殊的規則來控制如何乘所有的虛單位。這就是用“範諾平面”的圖形表示出來的:
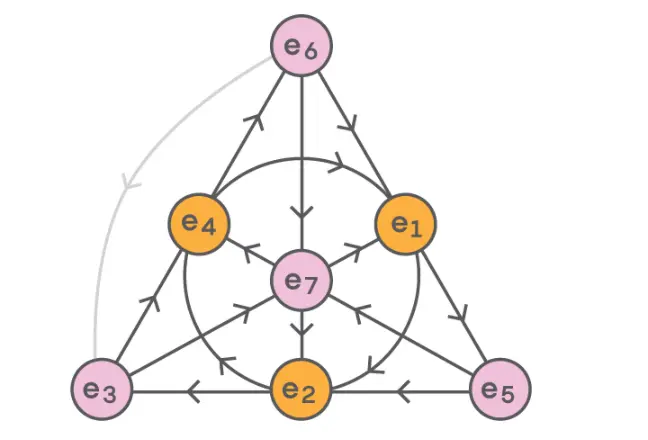
在四元數的表示中,沿著箭頭方向相乘得到的是正乘積,而沿著反箭頭方向相乘得到的是負乘積。
像四元數一樣,八元數乘法是不可交換的。此外八元數也不滿足結合律,當將三個八元數x、y、z相乘時,(x × y) × z = x × (y × z)並不一定是正確的。例如,用上面的圖表,我們可以看到:
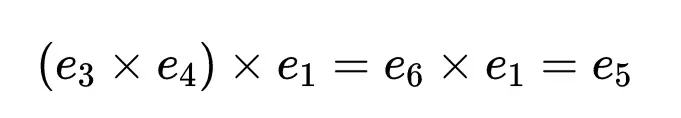
但:
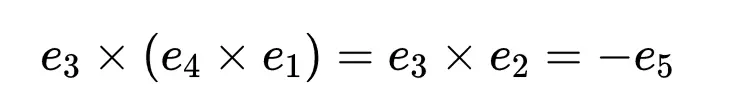
現在我們有了一個不滿足交換律、不滿足結合律的數字系統。它有什麼用呢?一些物理學家認為八元數可能是描述強、弱和電磁力如何作用於誇克、輕子和它們的反粒子的關鍵。如果這是真的,這將有助於解決現代物理學中最大的謎團之一。
通過不斷地擴展實數來創建更大的數字系統(複數、四元數、八元數),在這些系統中我們可以加、減、乘、除,每一次擴展都會有損失(四元數損失了交換律,八元數進一步損失了結合律)。在這個過程中,我們也可能與我們認為真實的東西失去聯繫。但我們得到的是思考世界的新方式。我們總能找到它的用處。
轉載請超鏈接註明:頭條資訊 » 現實邊緣的數字,從四元數到八元數,將成為解決物理學困境的關鍵
免責聲明
:非本網註明原創的信息,皆為程序自動獲取互聯網,目的在於傳遞更多信息,並不代表本網贊同其觀點和對其真實性負責;如此頁面有侵犯到您的權益,請給站長發送郵件,並提供相關證明(版權證明、身份證正反面、侵權鏈接),站長將在收到郵件24小時內刪除。