我們人類生活在一個三維世界中。作為三維生物,沒有什麼比四維生物更可怕了。對我們來說,它們就像神,如果它們稍稍有點邪惡,就可以隨心所欲地摧殘和毀滅我們。
面對四維生物,人類沒有任何物理裝備和心理裝備,所以任何更高維度的生物對我們來說都具有先天戰術優勢。
漫畫集《奇幻故事之1963》(1963-Tales of the Uncanny,出版於1993年)在描述跨維度的戰爭時還算比較準確。在故事《它來自……高維空間!》(It Came from...Higher Space!)中,來自四維空間的生物攻擊了一位三維空間的受害者。
漫畫中的怪物由很多懸浮、分離的肢體構成。它在空中飛行,做出各種變形。
每當這隻怪物出現時,半空中先出現一縷煙霧,然後煙霧像氣球一樣膨脹為三維體。作者將它描繪成一個肉做的甜甜圈,真是倒胃口。

想象一下三維生物攻擊二維生物的情形,我們就可以解釋為什麼四維怪物的身體可以分離。
處於三維空間中意味著我們可以在3個不同的方向運動:左右、前後、上下,而二維生物只能在兩個方向上移動:它們被限制在一個平面上。
讓我們想象一個完全平的二維外星生物,姑且將其命名為平星人(hypoflatical),假設它們生活的宇宙是一個極其薄的平面。對我們來說,它們的宇宙就如同一張紙。我們可以從上方或下方悄悄地靠近它們的宇宙。
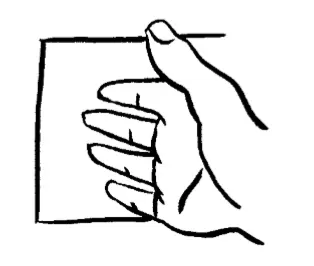
由於它們對第三維度沒有概念,它們不知道我們在哪裡。
三維空間為我們提供了完美的偽裝。是時候向二維生物發起我們的恐怖襲擊了,我們需要做的僅僅是從第三個方向進入它們的二維宇宙。
現在切換到平星人的視角。當我們的手指穿透它們的二維世界,它們會看到幾個懸浮的圓盤漸漸變大、接近。
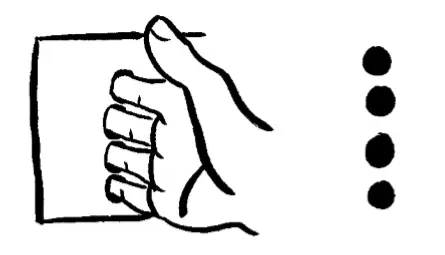
進而當手掌進入二維世界,這些圓盤便會合並起來。平星人只能看到我們手的二維截面,它就像在空中飛的肉餅。

(二維平面旁邊的手不會被發現。只有當手逐漸穿過二維世界,它與二維世界相交的部分才會被平星人看到)
平星人躲起來也沒用:作為三維生物,我們可以像看平面設計圖一樣看到整個二維世界——阿蘭·摩爾故事中的四維生物也是這樣看待我們三維世界的。
因此,平星人沒法躲到什麼東西後面,也沒法把自己鎖進安全的角落。對我們來說,進出封閉的二維世界如同進出二維正方形那樣簡單。

我們還可以清楚地看到二維生物的內部:它們體內的所有器官都會展現在我們面前,任我們擺佈。
這正是四維生物對三維生物造成的威脅:它們潛伏在三維宇宙旁邊,靜靜地觀察我們的一舉一動和我們身體的所有部件;它們可以輕而易舉進入我們的身體,並從內部將我們殺死。

這些怪物是我們的噩夢,不過幸好,沒有證據表明四維生物是存在的,但對四維空間多些瞭解並沒有什麼壞處,以防萬一嘛。
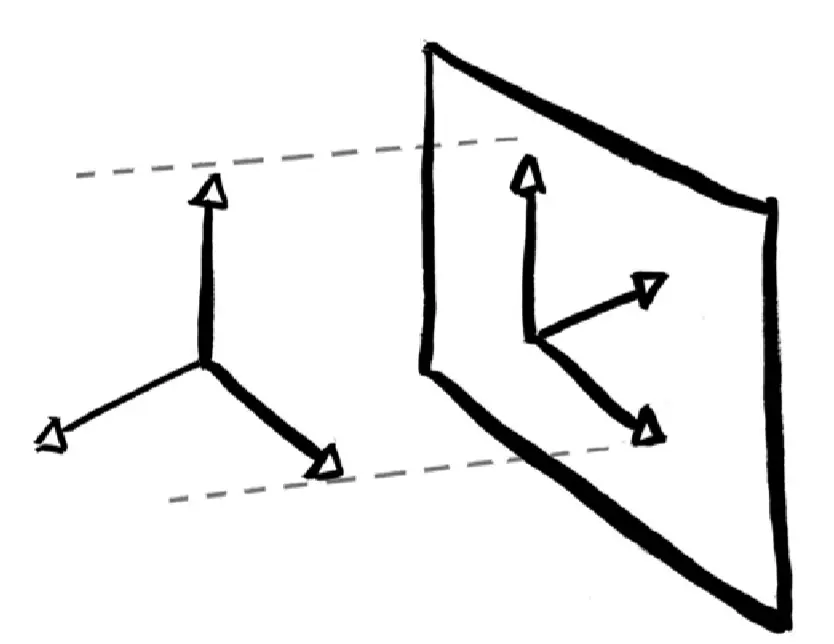
假如我們是仁慈的三維生物,本著跨維度交流的善意,欲向平星人展示我們的三維世界—向它們講解它們之外的世界是什麼樣的,例如,向它們展示三維立方體。
如果我們將立方體移入平星人的二維世界,它們只會看到各種不同的截面。最無趣的方式是先推入正方體的一個面,這樣只能讓它們看到一個正方形突然出現,然後又突然消失。
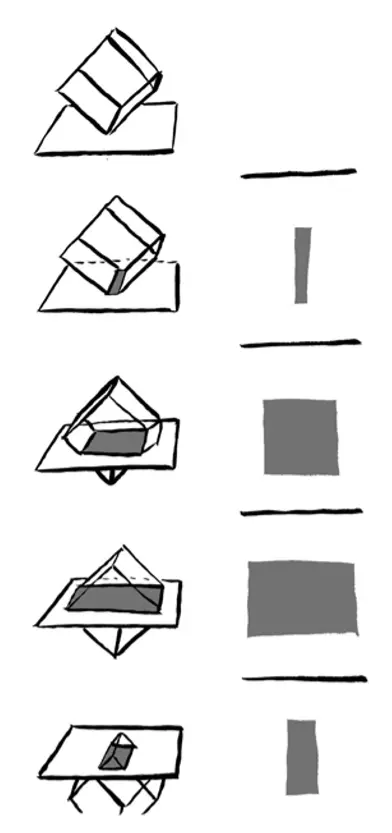
(當三維立方體從一條邊開始穿越二維平面時,平星人看到的景象)
稍微有趣的方式是先推入一條稜,這樣它們會看到一個長方形從無到有,慢慢變大,然後再慢慢縮小到無。
不過最有趣的方式是先推入一個頂點,平星人會看到一個三角形從無到有,慢慢變大,接著三 角形會發生各種形狀的變化,最終又收縮到無。對於限制在平面上的平星人來說,這是再新奇不過的事了。
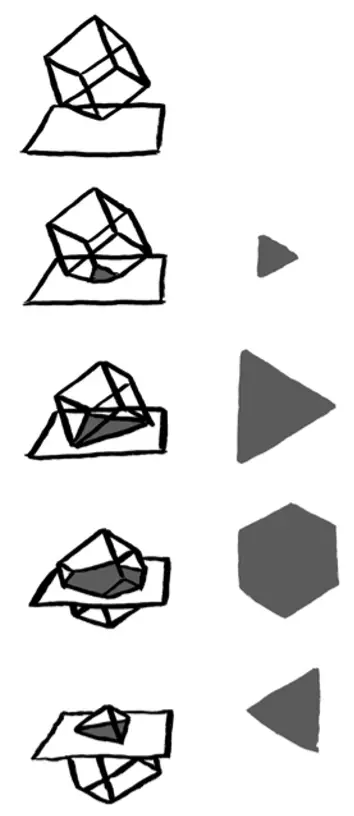
(當三維立方體從一個頂點開始穿越二維平面時,平星人看到的景象)
而且我們還會發現,這種進入方式和我們提到過的一個數學問題有所關聯:
如果我們能夠跟蹤記錄變化截面覆蓋過的所有區域,它會是一個完美的正六邊形;不僅如此,它恰好是我們在解決魯珀特王子的立方體穿過難題時遇到的立方體截面圖。
現在,讓我們來仔細思考四維超立方體(hypercube)穿越我們的三維世界會發生什麼事情。
假設一個友善的四維生物也本著跨維度交流的善意,向我們展示四維超立方體。當超立方體穿越我們的三維世界時,我們會看到它的一系列三維截面。



滑動看情緒逐漸暴躁的四維圖形
最無趣的方式仍然是從面開始穿越,我們只能看到一個普通的三維立方體突然出現,然後又突然消失。
如果超立方體從稜開始穿越,事情就變得有趣得多了。我們會看到一個三稜柱從無到有,慢慢變大,然後變形為六稜柱,接著再變成與之前方向相反的三稜柱,最終慢慢消失。
最有趣的仍然是超立方體從一個頂點開始穿越我們的三維世界。
此時,一個四面體憑空出現並均勻地變大,然後變形成一個由六邊形和三角形組成的奇怪圖形,有那麼一瞬間變成了正八面體,然後又倒著變回了之前的那些圖形(只不過方向相反),直至縮小消失。
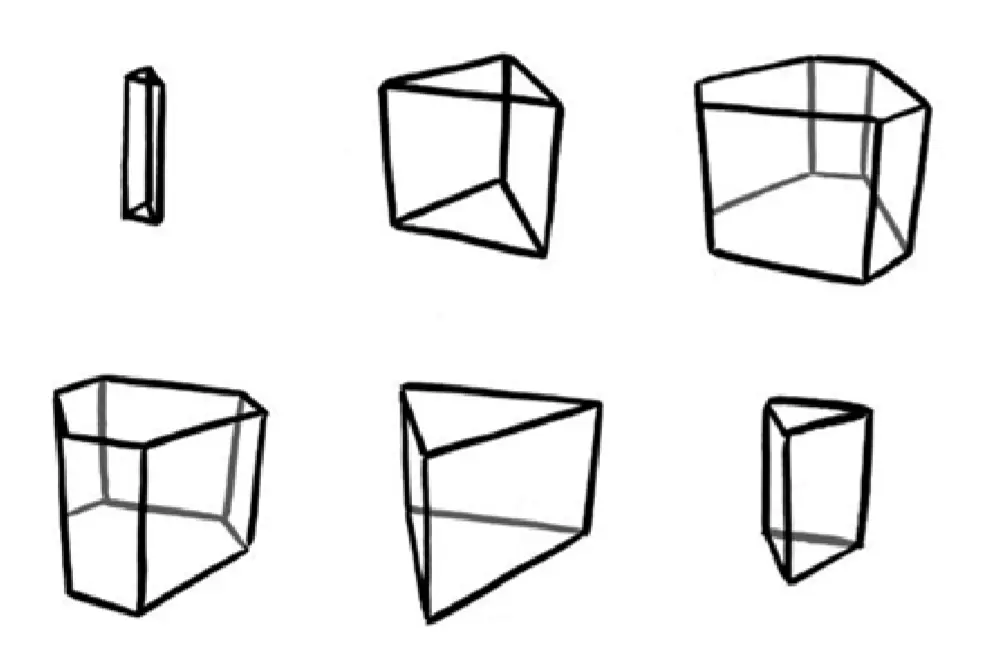
(當四維立方體從稜開始穿過我們的世界時,三維截面的變化情況。其覆蓋的所有空間會形成一個六稜柱)
我覺得這才能算作高大上的形象嘛。
我們再次探討一下穿越過程中出現的各種形狀。如果你把四維立方體分成完全相同的兩半,去尋找最大的三維截面,你會得到一個正八面體的截面,也就是三維立方體的對偶圖形。
在穿越三維空間的過程中,四維立方體覆蓋的所有空間會形成一個菱形十二面體(rhombic dodecahedron)。
然而,所有這些都無法告訴我們四維立方體的全貌。多說無益,讓我們一起動手做出這些形狀的模型吧。
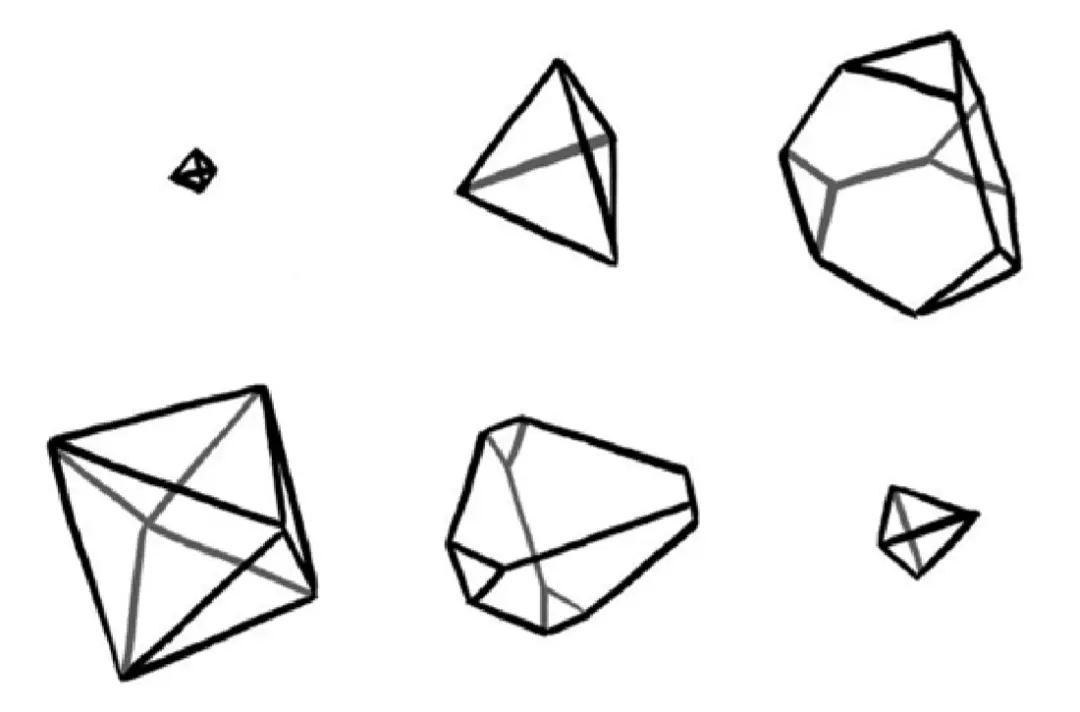
(當四維立方體從頂點開始穿越我們的世界時,三維截面的變化情況。有趣的是:在穿越過程中,四維立方體覆蓋的所有空間會形成一個菱形十二面體)
現在我們可以用吸管來構建一個四維立方體。和製作空間填充維埃爾——費倫模型時一樣,我們仍使用彩色吸管,但在這裡,不同的顏色代表不同的方向。
讓我們先從低維開始,然後不斷增加維數。製作一個一維圖形非常容易:一根吸管就是一個一維圖形。我們用紅色代表唯一的方向。

(一維的線)
製作二維圖形也沒有增加多少難度。和先前一樣,我們用彎曲的吸管刷來連接紅色吸管(代表水平方向)和藍色吸管(代表垂直方向)的末端。
這時我們可以在兩個方向自由移動。其實對於平星人來說,這也是輕而易舉的把戲。
我們可以這樣理解二維正方形:將一維的邊複製成兩條,然後將它們用另外一方向的兩條邊連接起來。

(二維的正方形)
類似的,三維立方體可以理解為將二維正方形複製了一次,然後將兩個正方形的頂點通過第三個方向上的新邊連接起來。
因此,你只需要按照剛才的配色再做一個正方形,然後用另一種顏色的吸管(比如綠色)將兩個正方形的頂點對應連接起來,便能得到三維立方體模型了。
出於習慣,你可能會將模型做成直立的。然而,為了向平星人展示立方體,我們可以將立方體壓扁在一個平面上。
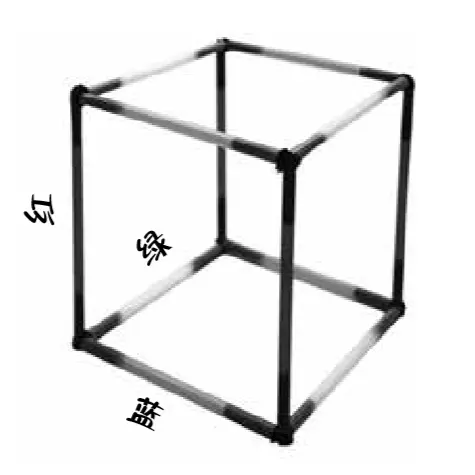
(三維的立方體)
為了使立方體變成四維的,我們要複製一個立方體,然後將這兩個立方體的頂點用另一種顏色的吸管(比如黃色)連接起來,這種顏色就代表第四個方向。這個模型和我們向平星人展示的立方體類似。
在我們展示三維立方體時,第二個正方形本該被抬離二維平面變成三維,但是我們把它壓到了第一個正方形的旁邊。
在這裡,第二立方體本該被抬離我們的三維曲面,進入第四維,但是我們讓它落在第一個立方體的旁邊。
這個模型是一個完整的四維立方體,只不過為了適應我們可憐的三維世界,被壓平了。
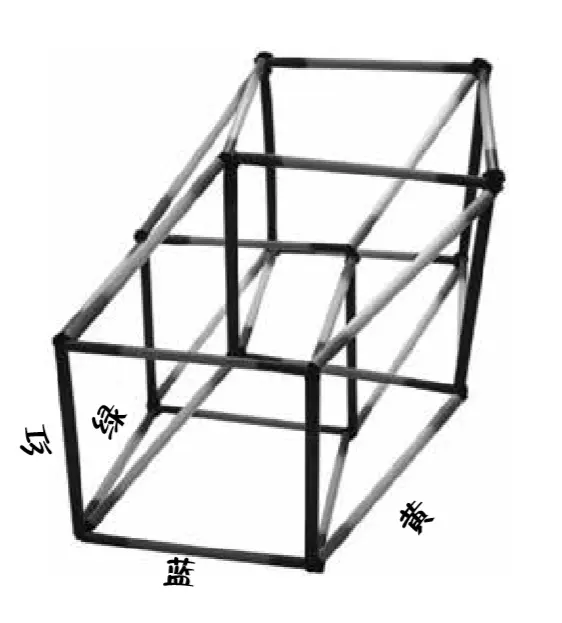
(四維超立方體)
平面版的三維立方體形狀和立方體的投影相同。如果我們利用光將三維立方體投影到一個平面上,就能看到它的二維投影,而這正是平星人看到的三維世界。
仁慈的四維生物也可以用同樣的方式將四維圖形進行投影,向我們展示它的三維投影:你製作的四維吸管立方體模型便是四維立方體的一個三維投影。
不過我們還可以通過另一種方式得到投影:引入透視。如果將三維立方體的第二個正方形縮小一點,使其懸浮在第一個正方形內部,便可得到立方體的平面投影,邊與邊之間不會相交。

同樣,我們也可以將四維立方體的第二個三維立方體做小一些,使其懸浮在第一個立方體內部,從而獲得四維立方體在三維空間的投影,面與面之間不會相交。
是不是有似曾相識的感覺?你在這之前確實見過類似的四維立方體——立方體狀肥皂泡。當時你已經在不經意間用肥皂膜做出了一個四維立方體的三維投影。
除了通過透視來研究高維圖形,我們還可以通過研究旋轉立方體的投影。
為了獲得旋轉三維立方體的二維投影,將其中一組相對的面染上顏色,將其他4個相鄰的面留白,這樣可以幫助我們跟蹤立方體的旋轉。

(加入些許透視,便可避免圖形的自相交)
我們還可以利用這個旋轉的投影向平星人展示三維立方體。雖然立方體在平星人二維宇宙旁邊的三維空間旋轉,但平星人能夠通過正方形的投影做出判斷。
影子越來越大,表明正方體正在向它們靠近;反之,投影越來越小,表明正方體正在遠離它們。
不幸的是,在它們看來,兩個正方形不斷穿過對方。所有的解釋都無法讓平星人看到這兩個 正方形在更高的維度中沒有相交,而是處於前後不同的位置。
(旋轉三維立方體的二維投影和旋轉四維立方體的三維投影,上下兩張圖同時轉完半圈)
同樣,我們也可以將旋轉的四維立方體投影到三維世界。我們仍然將其中一組相對的立方體染色,起連接作用的其他立方體則是透明的。
當這個四維立方體在我們的三維宇宙之外旋轉時,每個立方體離我們更近時都會變大,離我們更遠時都會變小。
遺憾的是,和平星人一樣,在我們看來,這兩個方體不斷相交,但實際上,這兩個立方體在四維空間中屬於前後的關係,只是我們無法看到這一點。
當三維立方體的一個二維面剛好與影子所在的二維平面垂直時,它的投影會短暫地消失。

(一個沒有復原的四維魔方)
同樣,當四維立方體的一個三維立方體恰好與我們的三維宇宙垂直時,它也會從我們的視線中短暫消失。
不可思議的第四維度!
如果你想自己試著轉一轉四維立方體,我建議你嘗試研究四維魔方(Rubik’s Cube)。
三維魔方需要將顏色相同的二維色塊移動到三維立方體的同一個二維面上,但四維魔方有些不同,你需要將顏色相同的三維色塊移動到四維立方體的同一個三維面上。
你無法直接變換四維立方體,但是你可以通過拖拽四維魔方的三維投影來間接地進行變換,這種魔方可以在網上找到。
玩的時候你腦子會特別暈,因為三維投影可以在我們熟悉的三個方向上運動,但四維立方體還能在第四個正交(orthogonal,即交角為直角)的方向上旋轉(網站上是通過按住shift鍵實現的)。
不過有點糟糕的是,因為你只能在電腦屏幕上看到四維魔方的三維投影,所以實際上你處理的是四維立方體的三維投影的二維投影,我只能祝你好運了。
來源:遇見數學
編輯:荔枝
轉載請超鏈接註明:頭條資訊 » 高維生物的快樂你真的想象不到嗎
免責聲明
:非本網註明原創的信息,皆為程序自動獲取互聯網,目的在於傳遞更多信息,並不代表本網贊同其觀點和對其真實性負責;如此頁面有侵犯到您的權益,請給站長發送郵件,並提供相關證明(版權證明、身份證正反面、侵權鏈接),站長將在收到郵件24小時內刪除。