曉查 賈浩楠 發自 凹非寺
量子位 報道 | 公眾號 QbitAI
一個多月前,著名英國數學家約翰·康威(John Conway)因患新冠肺炎逝世。
斯人已逝,但他留給了世界豐富的知識遺產,最知名的莫過於“生命遊戲”,還有一個困擾數學界50年的難題“康威扭結”(Conway Knot)。
令人意想不到的是,最近這個問題被德州大學奧斯汀分校的一位博士小姐姐Lisa Piccirillo解決了,而且她只用了一週的業餘時間。

△ Lisa Piccirillo
Lisa本人也因此獲得了MIT的tenure-track預聘職位,前途無量。
其實這篇論文最早是Lisa在2018年讀博期間完成的,當Lisa偶然得到這個結果的時候,她並沒有意識到這個問題的重要性。
有一天,她把自己的解決方法告訴了同在德州大學奧斯汀分校的Cameron Gordon教授。Gordon教授大叫道:“什麼?我現在就要去投頂級期刊!”
這一舉動甚至嚇到了Lisa。
直到今年2月,這篇文章才被刊登在學術雜誌《數學年刊》上。想必康威在得知自己提出的問題被解決後,也會感到欣慰吧。
什麼是扭結
「結」這個概念,在日常生活中常被看成是一根有頭有尾的繩子打成的結。但數學家眼中的「結」,是一個首尾相連的閉環結,這種結是無法被解開的。

自上個世紀以來,有關扭結的研究啟發了量子力學、DNA結構和三維空間拓撲學。
所以數學家們自然要發問,在4維空間中是否有與三維空間對應的扭結理論。
但是這裡存在一個問題:在第四個維度上,扭結的繩體可以互相重合穿越,這樣一來,任何扭結都可以解開了。

所以4維空間的扭結不是三維扭結的簡單移植。
4維空間的扭結並不好理解,我們可以藉助3維空間中的的一個球體來想象。
如果切開一個3維球體,可以得到一個未打結的圓環。切開一個4維空間的扭結球體,你可能看到一個打結的環,或者是一個未打結的閉環。
任何能用這種「切開」一個扭結球體而得到的扭結,都稱它們為「可切的」(slice),即片狀結。但也有一些「不可切」的扭結,比如有3個交叉的三葉結。
片狀結提供了3維和4維扭結理論的橋樑。
在4維拓撲學中,片狀結有兩種形式,一種1980年代年提出的理論認為,在4維空間中,不只有我們常規認知的平坦光滑球體,還普遍存在一種皺縮球體,且永遠無法被拉平。所以4維空間中的扭結是否可切,取決於這些特殊的皺縮球體。
這種皺縮的球體並不是4維空間的異常,而是一個十分有用的特徵。4維空間中的片狀結是「拓撲可切」,而不是「平滑可切」。
這意味著數學家可以藉此構造不同版本的普通四維空間,這種4維空間在拓撲學上與其他沒有不同,只不過是褶皺的。

切片性問題是這些奇異的四維空間的 “最低維度探究”。
康威扭結
多年來,數學家們發現了形形色色的扭結,這些結在拓撲學上可切,但並不是平滑可切。然而,這些扭結的交叉都大於12。而在交叉點數小於12的扭結中,只有康威結的切片狀態卻一直無法找到。

△劍橋大學牛頓數學科學研究所的大門,用康威扭結來做裝飾
康威在上世紀50年代時對扭結理論產生了濃厚的興趣。
他想出了一個簡單的方法,把交叉點數目不同的的扭結一一列出來,而前人將這項工作推進到10個交叉的扭結。
康威列出了所有具有11個交叉點的扭結,很快發現了它們的特殊之處,這些就是康威扭結。
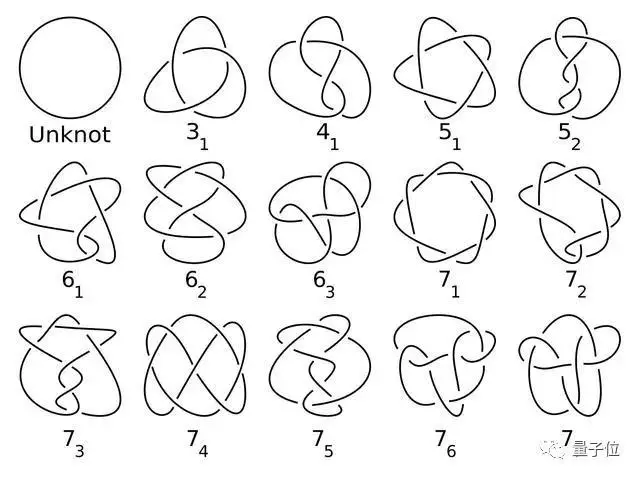
△圖中只畫到了7個交叉的扭結,交叉點是兩條繩體交叉之處
11個交叉點的康威扭結,是拓撲可切的,但數學界一直無法證明它是否平滑可切。
數學家馬克·休斯(Mark Hughes)創建了一個神經網絡,利用扭結的不變量和其他信息來預測可切性等特徵。對於大多數的結,這種神經網絡能夠做出明確的預測。但它對康威結是否具有平滑可切性卻沒有確切答案。
康威扭結是否平滑可切之所以如此重要,不僅因為它困擾了數學界半個世紀。
平滑可切的扭結為數學家提供了一條探索四維空間奇特屬性的途徑。
而證明康威扭結是否為平滑可切,已經成為扭結理論重大突破的硬標準。
問題解決
數學家一直懷疑康威結不是平滑可切的,因為它缺乏一種 “帶狀性 “的特徵,而平滑可切的扭結通常具有這種特徵。
但康威結也有一個特點,使它對所有試圖證明它不是光滑切片的嘗試都無功而返。
康威扭結有一種變體,如果我們把康威扭結畫在紙上,把它的下半部分剪下來,翻轉180度再接上,那麼就得到一個Kinoshita-Terasaka扭結。
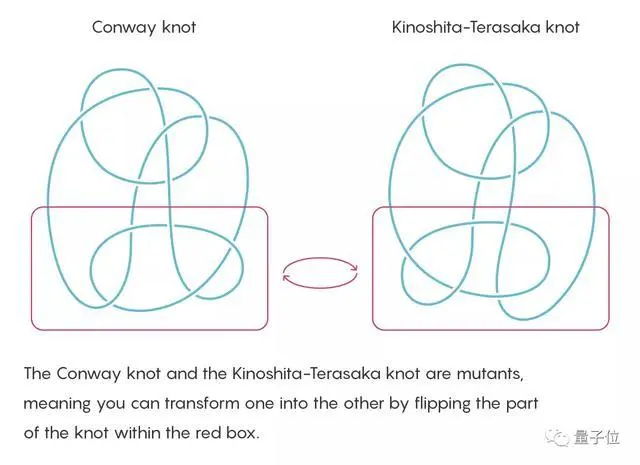
巧合的是,後面的扭結是平滑可切的。
Lisa本人喜歡扭結理論所需的視覺直覺,但她並不是扭結理論方面的專家。Lisa在波士頓大學讀本科期間的老師Elisenda Grigsby,Lisa當時並沒有展現出天才少年的潛質,但是她的創造力吸引了Grigsby教授的注意。
Grigsby教授說:“她非常相信自己的觀點,並且一直如此。”
Lisa當時正在思考關於康威扭結的問題,當時她正在考慮除了突變外將兩個結關聯起來的另一種方式。每個扭結都有一個關聯的四維形狀,它是通過將結放置在4D球的邊界上並沿著結在球上縫製某種帽而製成,數學家稱之為跡(trace)。
Gordon表示,跡以一種非常強烈的方式編碼了扭結。
不同的結可以具有相同的四維跡,數學家發現相同跡的扭結總是具有相同的可切性質:要麼都是可切的,要麼都不是。但是Lisa和萊斯大學博士後Allison Miller證明,可以將扭結跡的不變性讓我們在研究扭結可切性質的時候,構造相似扭結變得非必要。
這為Lisa證明康威扭結非平滑可切提供了一種策略:如果可以為康威扭結構造一個相同跡的扭結,那麼也許可以更好地與可切不變性配合使用。

構造這樣同跡的扭結並非易事,但是Lisa卻有非常的天賦,她只是回到家中研究就做到了這一點。
通過巧妙的扭結的組合,Lisa設法構造了一個複雜的扭結,它的跡與康威扭結相同。Lisa使用了一種叫做拉斯穆森S不變量(Rasmussen’s s-invariant)的工具,結果顯示她構造的扭結不是平滑可切的,因此康威扭結也不是。
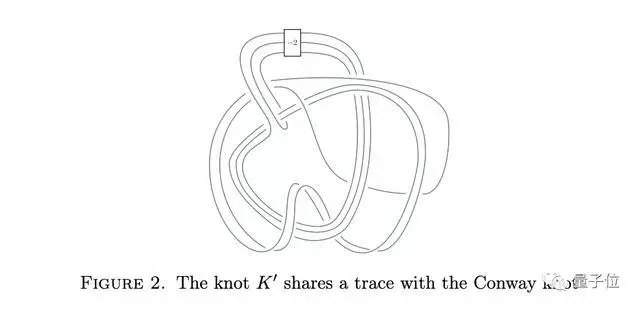
“這是一個非常美麗的證明,”戈登說。沒有理由指望Piccirillo構造結會產生拉斯穆森的小號 -invariant,他說。“但是它起作用了……有點令人驚訝。”
Gordon給了Lisa很高的讚譽:“這是一個非常美麗的證明。”他完全沒想到Lisa用這樣一種用具實現了證明。
Lisa的本科論文導師Greene說:Lisa的工作說明拓撲學家對扭結跡的認識還存在著不足。
轉載請超鏈接註明:頭條資訊 » 困擾數學家50年的問題,竟被博士小姐姐用一週業餘時間解決了
免責聲明
:非本網註明原創的信息,皆為程序自動獲取互聯網,目的在於傳遞更多信息,並不代表本網贊同其觀點和對其真實性負責;如此頁面有侵犯到您的權益,請給站長發送郵件,並提供相關證明(版權證明、身份證正反面、侵權鏈接),站長將在收到郵件24小時內刪除。