299792458m/s,現在,我們可以輕易地得到光速的準確數值。但是直到近代以前,人們對光的速度都缺少一個準確的認識。甚至都不能確定光速到底是無限的,還是以極快的有限速度傳遞。

來源 | 新浪
對這個問題,據目前已發現的文獻記載,對光速的最早研究甚至可以追溯到古希臘時期。
歷史記載,恩培多克勒(前490年-前430年)是第一個宣稱光速有限的人。他相信光是一種運動的東西,所以運行需要時間。
古希臘、伊斯蘭世界以及歐洲經典學者都對此進行了長期的討論。直到1676年,奧勒·羅默首次對光速進行測定,才有了光速有限的結論。
1
早期測量
1638年,著名科學家伽利略提出一項他曾經做過的實驗。伽利略一行四人,分成兩組,分別登上兩座相隔甚遠的山峰,每組各自攜帶一個光源——煤油燈。
他對煤油燈做了一個簡單的改進,就是在煤油燈的一面加了一個滑蓋,這樣關閉滑蓋,燈光就被擋住,如果把滑蓋拉起,燈光就會照射出來。通過快速地拉動滑蓋,就能讓煤油燈一亮一滅,製造出看上去在閃爍的效果。
在伽利略的實驗中,除了兩盞煤油燈外,還需要兩隻一模一樣的鐘擺計時裝置,以及記錄數據的紙筆。他打算利用兩邊記錄燈光開啟關閉時間的方法來測算光的速度。

來源 | 百度
我們已經得知光速大約是30萬千米每秒,而人的反應時間大概是240ms左右。因此我們幾乎可以斷定,伽利略的這個實驗是測不出光速的。
事實也是如此,意大利佛羅倫斯的實驗學會(Accademia del Cimento)於1667年進行了伽利略的實驗。在兩盞燈相距約一英裡的情況下,沒有觀察到任何的延時。
我們把今天已知的光速數值代入這個實驗進行計算,可以得出延時只有11微秒,這已經超越了人類反應的極限了。
很顯然,伽利略並沒有測出光速,他得到的結論是:就算光速是有限的,它也肯定快得不可思議。而第一個測出一個比較靠譜數據的人,是奧勒·羅默。
1676年,奧勒·羅默首次對光速進行了測定。
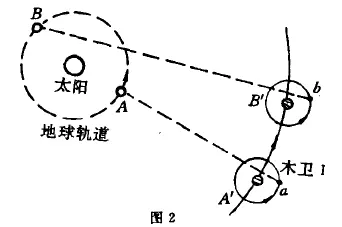
羅默觀察木星的衛星木衛一,木衛一繞木星公轉,繞到木星背後時被遮住就會出現衛星蝕。隨著地球在公轉軌道上移向木星,在地球上觀測到木衛一蝕之間的時間間隔將逐漸變短;而當地球遠離木星時,木衛一蝕的間隔則逐漸變長。
簡單介紹一下這種方法。首先由中學物理知識我們可以知道,木衛一是繞木星作勻速圓周運動的,那麼木衛一衛星蝕的週期應該是不變的。
羅默根據這些數據計算出,當地球距離木星最近時,木衛一蝕將比按照公轉週期預測的時間提前約11分鐘出現。而六個半月後,當地球距離木星最遠時,木衛一蝕將比預期的時間晚11分鐘出現。累加時間點相差高達22分鐘!他意識到,這22分鐘就是光在地球公轉軌道上傳播的時間。

來源 | 新浪
後來,克裡斯蒂安·惠更斯利用這一數據加上對地球公轉直徑的估值,計算出光速大約為22萬千米每秒,這一數據約有26%的誤差。
艾薩克·牛頓(Isaac Newton)在其1704年出版的《光學》一書中描述了羅默對光速的計算,並給出了光從太陽到地球傳播所需的時間為“七到八分鐘”。
羅默和惠更斯的結果和實際相差非常巨大。直到19世紀,阿曼德·斐索發明了旋轉齒輪法,並得出了315000 km/s的光速數值。萊昂·傅科進一步完善了斐索的方法,在1862年所得出的數值為298000 km/s。這一數據已經非常接近準確值了。
2
旋轉齒輪法
簡單解釋一下旋轉齒輪法。
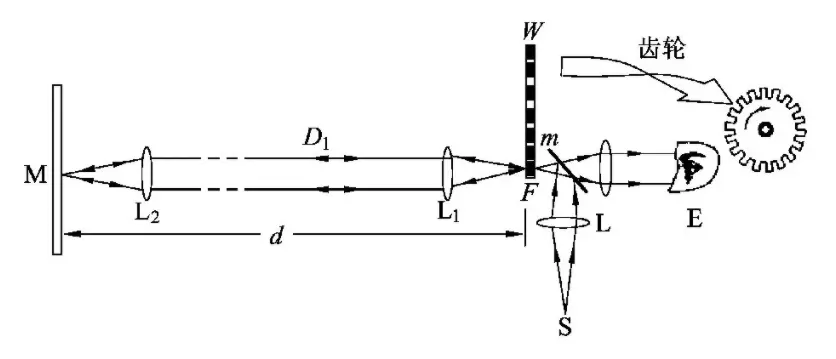
旋轉齒輪法
來源 | 《對旋轉稜鏡法和旋轉齒輪法測光速的討論》
按照上圖將實驗用具擺放,當齒輪靜止不動時,光線穿過透鏡L進入人的眼睛當中。先緩慢轉動齒輪W,由於光線會被齒輪所遮擋,我們會看見明暗相間的像(如下圖乙)。將齒輪調整到一定的轉速,使其在第一個縫穿過經過反射回來時,能恰好被相鄰的第一個齒輪遮擋(如下圖丁)。
這樣,我們就不能看見光線了。此時,通過計算轉速、光程、齒數,我們就能得到光速了。
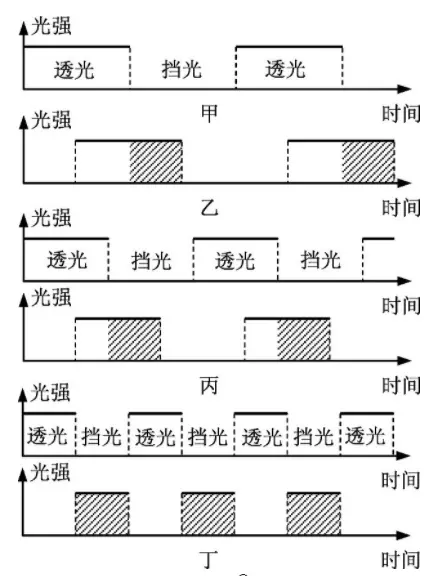
旋轉齒輪法原理
來源 | 《對旋轉稜鏡法和旋轉齒輪法測光速的討論》
3
旋轉稜鏡法
後來,邁克爾遜憑藉旋轉稜鏡法得到了更準確的數值。
旋轉稜鏡法
來源 | 《對旋轉稜鏡法和旋轉齒輪法測光速的討論》
他選擇了兩個山峰,測出兩個山峰間的距離,在第一個山峰上安裝了一個強光源和一個正八面稜鏡。
由強光源發出的光經過狹縫射在八面鏡的鏡面1上,被反射到放在第二個山峰的凹面鏡上,再由凹面鏡反射回第一個山峰。如果八面鏡靜止不動,反射回來的光就在八面鏡的鏡面3上再次反射,經過望遠鏡,進入觀測者的眼中。
我們將光線假想為粒子,第一個粒子在經過稜鏡1號面反射後,我們令稜鏡以較小的轉速轉動。當該粒子經過遠處的反射鏡反射回來時,3號面已經不再與光線成45度角。此時該粒子無法進入觀察者眼睛,因此觀察不到光源的像。
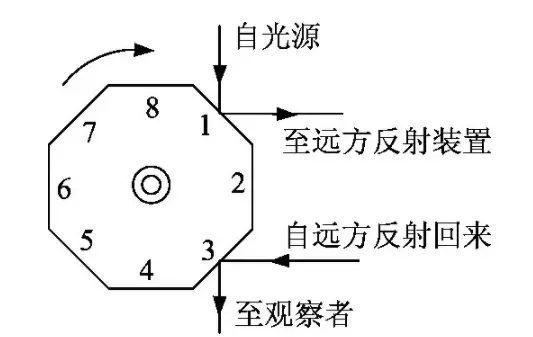
旋轉稜鏡法
來源 | 《對旋轉稜鏡法和旋轉齒輪法測光速的討論》
若緩慢提高稜鏡轉速,當光線反射回稜鏡時,稜鏡剛好轉過1/8轉,即2號面轉至原3號面所在位置,則光線又可以進入觀察者眼睛,使觀察者重新看到光源的像。這樣,稜鏡轉過1/8的時間,就是粒子從1號面經過反射,回到3號面的時間。
光線可以理解為源源不斷的粒子束,當我們將稜鏡調整到合適的轉速時,便能看見不斷閃爍的像。由於視覺暫留效應,我們能看見持續的像,這一點對於觀測也有一定影響。
總之,在旋轉稜鏡法中,根據八稜鏡轉過1/8所用的時間和兩個山峰之間的距離,就可以算出光速。邁克爾遜經過矯正之後,在1926年測出的光速是299796000 m/s,離真實數據已經非常接近了。
上述方法基本都停留在光學測量的層次,在麥克斯韋方程組出現後,人們意識到光也是屬於電磁波的一種。既然屬於電磁波,那麼通過測量光的頻率和波長,根據c=λf,其中f是頻率,λ是波長(m),自然就能得出光速了。
4
光速不變
光速是測出來了,但新的問題又出現了。
既然光速是有限的,根據伽利略的相對性原理,速度都是相對的,以不同的參考物測出的速度是不同的。並且速度是可以疊加的。例如:假設人相對於地面的速度是5 m/s,高鐵相對於地面的速度是83m/s,那麼人在高鐵上與高鐵同向行進時,相對於地面的速度就是88m/s。
那麼,你在地面上用手電筒射出的光線和你在高鐵上用手電筒射出的光線速度呢?難道二者速度也會不同嗎?
這個問題困擾了科學家們很久,直到麥克斯韋方程組的出現以及“光速是不變的”這個結論的得出——也就是光速不變原理,即光速相對於任何觀察者來說,都是不變的。
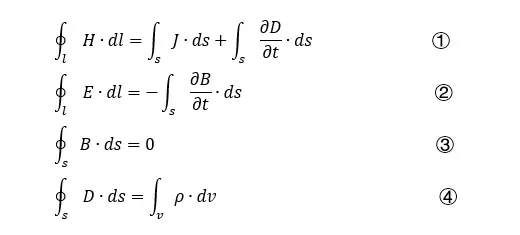
麥克斯韋方程組
如圖,利用大學物理知識以及微積分知識,可以得到光速的表達式。
式中,真空磁導率是一個常數:
真空電容率也是一個常數:
代入光速的表達式,我們可以直接計算出光速的大小。
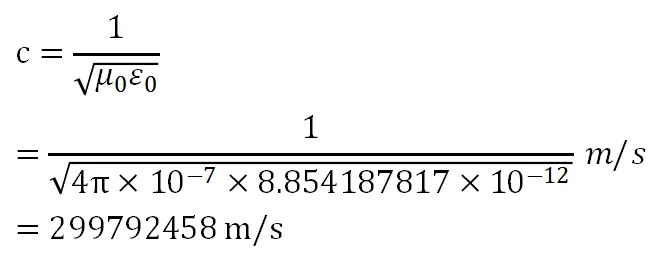
利用以上公式我們成功得到了光速的值,並且從理論上證明瞭光速是一個常數,並且它相對於任何觀察者來說,都是相同的。
來源 | 新浪
1905年,愛因斯坦總結了麥克斯韋等人的經驗,發表了著名的狹義相對論,狹義相對論中的一個基本公設就是光速不變原理。
1950年,艾森提出了用空腔共振法來測量光速。這種方法的原理是,微波通過空腔時它的頻率為某一值時發生共振。根據空腔的長度可以求出共振腔的波長,再把共振腔的波長換算成光在真空中的波長,就可以計算出光速。
1972年,埃文森得到了真空中光速的最佳數值:299792457.4±0.1 m/s。
既然光速是一個常數,於是1983年國際度量衡大會(CGPM)重新制定了米的定義:“光在真空中行進1/299 792 458秒的距離”為一標準米。
為什麼宇宙會將信息傳遞的最大速度限制在光速?
這個問題目前還無人能夠回答。能夠在1秒內繞地球轉七圈半,光速已經非常快了,但這一速度對於廣袤的宇宙來說,卻是如此之慢。
除太陽之外,距離我們最近的一顆恆星叫比鄰星,距離我們達4.22光年。就是說即使我們以光速旅行,到達比鄰星也要4年多的時間;而我們所在的銀河系,銀盤直徑約為100000光年;根據現有的宇宙模型計算,目前我們可觀測宇宙的直徑更是高達930億光年,並且還在不停地膨脹中。
在描述宇宙之時,我們用光年來作為長度單位,但哪怕是人類目前最快的飛行器——太陽神2號,達到的速度也不過是0.000234倍光速。

來源 | 新浪
隨著科技發展,或許在遙遠的未來,星際航行將不再是幻想,讓我們也能有機會體驗一把“接近光速”的感覺。
審核專家:吳寶俊
理論物理博士
來源:數字北京科學中心
編輯:jita
轉載請超鏈接註明:頭條資訊 » 光速這麼快,是如何被人類測出來的?
免責聲明
:非本網註明原創的信息,皆為程序自動獲取互聯網,目的在於傳遞更多信息,並不代表本網贊同其觀點和對其真實性負責;如此頁面有侵犯到您的權益,請給站長發送郵件,並提供相關證明(版權證明、身份證正反面、侵權鏈接),站長將在收到郵件24小時內刪除。