
相對於代數和函數等內容而言,幾何因其變化多端,更能考查考生的數學綜合能力,因此幾何相關的試題一直是中考數學的難點和熱點,也是失分重點。
幾何相關的試題,可難可易,可靜可動,通過對輔助線的設置,可以設計出一些立意新穎,構思巧妙,精彩紛呈的幾何試題,這些已經成為中考命題者的出題思路。
在初中幾何內容當中,空間與圖形一般包括這四個方面的內容:圖形的認識,圖形與變換,圖形與座標,圖形與證明。幾何試題在設置上肯定都是圍繞圖形和空間的內容進行展開,這四塊內容既有內在的聯繫,又有各自的特點和側重。
因此,在平時的學習過程中,大家一定要準確把握幾何各部分內容的要求,探索圖形的基本性質及其相互關係,進一步豐富對空間圖形的認識和感受,這樣才能幫助自己能更好理解幾何相關的知識定理和方法技巧,以及相關的題型。

幾何有關的中考試題講解分析,典型例題1:
已知:在△ABC中,∠ACB=900,點P是線段AC上一點,過點A作AB的垂線,交BP的延長線於點M,MN⊥AC於點N,PQ⊥AB於點Q,A0=MN.
(1)如圖l,求證:PC=AN;
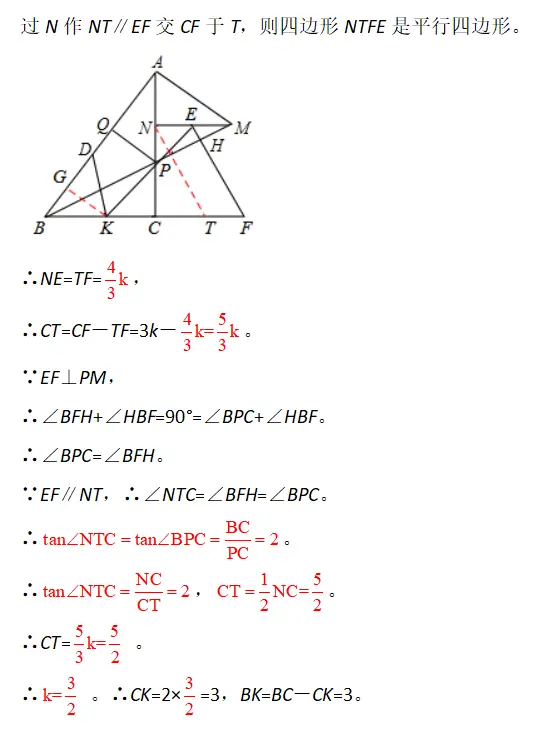
(2) 如圖2,點E是MN上一點,連接EP並延長交BC於點K,點D是AB上一點,連接DK,∠DKE=∠ABC,EF⊥PM於點H,交BC延長線於點F,若NP=2,PC=3,CK:CF=2:3,求DQ的長.
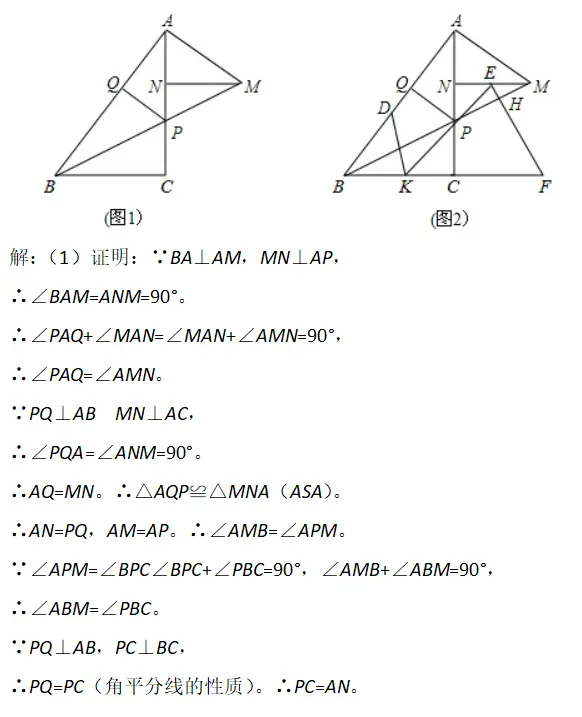


考點分析:
相似形綜合題,全等三角形的判定和性質,角平分線的性質,勾股定理,相似三角形的判定和性質,等腰直角三角形的判定和性質,解直角三角形。
題幹分析:
(1)確定一對全等三角形△AQP≌△MNA,得到AN=PQ;然後推出BP為角平分線,利用角平分線的性質得到PC=PQ;從而得到PC=AN。
(2)由已知條件,求出線段KC的長度,從而確定△PKC是等腰直角三角形;然後在△BDK中,解直角三角形即可求得BD、DQ的長度。

幾何有關的中考試題講解分析,典型例題2:
如圖,已知AB為⊙O的直徑,PA與⊙O相切於點A,線段OP與弦AC垂直並相交於點D,OP與弧AC相交於點E,連接BC.
(1)求證:∠PAC=∠B,且PA•BC=AB•CD;
(2)若PA=10,sinP=3/5,求PE的長.


考點分析:
切線的性質,勾股定理,圓周角定理,垂徑定理,相似三角形的判定和性質,銳角三角函數定義。
題幹分析:
(1)由PA為圓O的切線,利用切線的性質得到AP垂直於AB,可得出∠PAO為直角,得到∠PAD與∠DAO互餘,再由AB為圓O的直徑,根據直徑所對的圓周角為直角,可得出∠ACB為直角,得到∠DAO與∠B互餘,根據同角的餘角相等可得出∠PAC=∠B,再由一對直角相等,利用兩對對應角相等的兩三角形相似可得出△APD與△ABC相似,由相似得比例,再由OD垂直於AC,利用垂徑定理得到AD=CD,等量代換可得證。
(2)在Rt△APD中,由PA及sinP的值求出AD的長,再利用勾股定理求出PD的長,從而確定出AC的長,由(1)兩三角形相似得到的比例式,將各自的值代入求出AB的上,求出半徑AO的長,在Rt△APO中,由AP及AO的長,利用勾股定理求出OP的長,用OP﹣OE即可求出PE的長。
我們認真去研究這些幾何試題新特點,既有助於我們更好地理解知識定理和方法技巧的應用,認識不同題型之間的變化,又有助於我們更好地思考和提升中考複習效率。
中考壓軸題通常會以學生熟悉、感興趣、有價值的素材或數學活動為切入點,立足於知識、問題的生長點、發展點、延伸點,藉助操作活動、經驗、知識、思想方法等,重在考查考生髮現問題、提出問題、分析問題和解決問題的能力。
轉載請超鏈接註明:頭條資訊 » 提高數學成績,除了方法技巧,還有就是做好這件事
免責聲明
:非本網註明原創的信息,皆為程序自動獲取互聯網,目的在於傳遞更多信息,並不代表本網贊同其觀點和對其真實性負責;如此頁面有侵犯到您的權益,請給站長發送郵件,並提供相關證明(版權證明、身份證正反面、侵權鏈接),站長將在收到郵件24小時內刪除。