
在所有的中考數學壓軸題當中,跟動點有關的問題一直是繞不開的話題,縱觀全國各地的中考數學試卷,你會發現以動點作為壓軸題的考卷,數不勝數,這也充分體現了動點問題的重要性。
什麼是動點問題?
動點問題一般是指題目當中的圖形中存在一個或多個動點,它們在線段、射線或弧線上運動的一類開放性題目。幾何動態型問題就是在研究幾何圖形的運動中伴隨著一定的圖形位置、數量關係的“變”與“不變”性。就其運動對象而言,有“點動”“線動”和“面動”;就其運動形式而言,有“移動”“滾動”“旋轉”和“翻折”等。
如何正確求解動點類問題呢?
解決此類問題的關鍵是動中求靜,靈活運用有關數學知識解決問題。
大家要記住解動點問題的基本方法技巧是:
一是學會動中見靜;
二是學會動靜互化;
三是學會以靜制動。

動點有關的中考壓軸題,講解分析1:
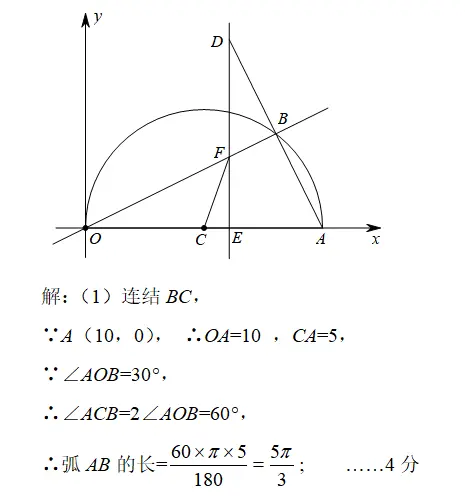
如圖,在平面直角座標系中,點A(10,0),以OA為直徑在第一象限內作半圓C,點B是該半圓周上的一動點,連結OB、AB,並延長AB至點D,使DB=AB,過點D作x軸垂線,分別交x軸、直線OB於點E、F,點E為垂足,連結CF.
(1)當∠AOB=30°時,求弧AB的長;
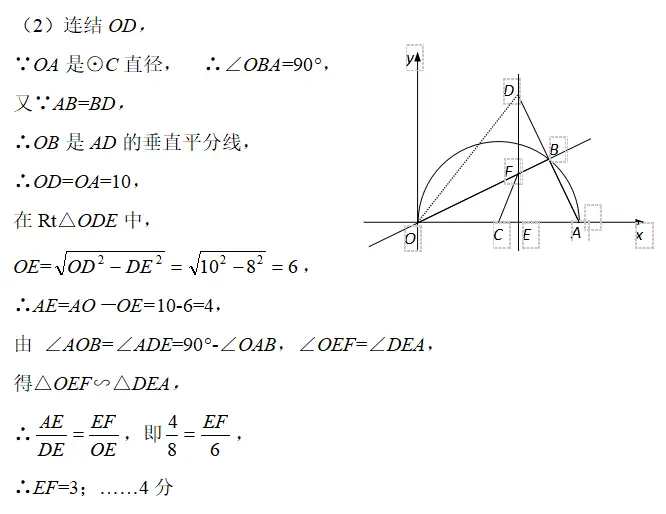
(2)當DE=8時,求線段EF的長;
(3)在點B運動過程中,是否存在以點E、C、F為頂點的三角形與△AOB相似,若存在,請求出此時點E的座標;若不存在,請說明理由.




考點分析:
相似三角形的判定與性質;座標與圖形性質;勾股定理;弧長的計算;平行線分線段成比例;代數幾何綜合題。
題幹分析:
(1)連接BC,由已知得∠ACB=2∠AOB=60°,AC=AO/2=5,根據弧長公式求解;
(2)連接OD,由垂直平分線的性質得OD=OA=10,又DE=8,在Rt△ODE中,由勾股定理求OE,依題意證明△OEF∽△DEA,利用相似比求EF;
(3)存在.當以點E、C、F為頂點的三角形與△AOB相似時,分為當交點E在O,C之間時,由以點E、C、F為頂點的三角形與△AOB相似,有∠ECF=∠BOA或∠ECF=∠OAB,當交點E在點C的右側時,要使△ECF與△BAO相似,只能使∠ECF=∠BAO,當交點E在點O的左側時,要使△ECF與△BAO相似,只能使∠ECF=∠BAO,三種情況,分別求E點座標.

動點有關的中考壓軸題,講解分析2:
在矩形AOBC中,OB=6,OA=4,分別以OB,OA所在直線為x軸和y軸,建立如圖所示的平面直角座標系.F是BC上的一個動點(不與B.C重合),過F點的反比例函數y=k/x(k>0)的圖象與AC邊交於點E.
(1)求證:AE•AO=BF•BO;
(2)若點E的座標為(2.4),求經過O.E.F三點的拋物線的解析式;
(3)是否存在這樣的點F,使得將△CEF沿EF對摺後,C點恰好落在OB上?若存在,求出此時的OF的長:若不存在,請說明理由.


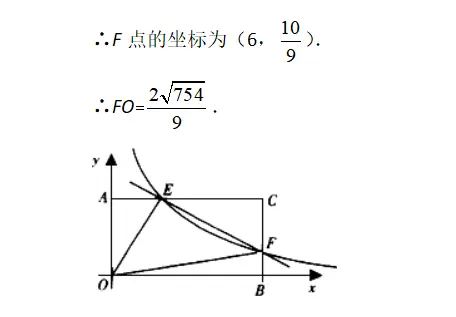
考點分析:
相似三角形的判定與性質;反比例函數圖象上點的座標特徵;待定係數法求二次函數解析式;矩形的性質;翻折變換(摺疊問題)。
題幹分析:
(1)根據反比例函數的性質得出,xy=k,即可得出AE•AO=BF•BO;
(2)利用E點座標首先求出BF=4/3,再利用待定係數法求二次函數解析式即可;
(3)設摺疊之後C點在OB上的對稱點為C',連接C'E.C'F,過E作EG垂直於OB於點G,則根據摺疊性質.相似三角形.勾股定理得出即可.
解題反思:
此題主要考查了反比例函數的性質以及待定係數法求二次函數解析式以及相似三角形的判定與性質,二次函數的綜合應用是初中階段的重點題型特別注意利用數形結合以及利用相似三角形的性質是這部分考查的重點也是難點.。
正確解決動點有關的壓軸題具體做法,可以分為三個步驟:
一是全面閱讀題目,瞭解運動的方式與形式,全方位考察運動中的變與變量及其位置關係;
二是應用分類討論思想,將在運動過程中導致圖形本質發生變化的各種時刻的圖形分類畫出,變“動”為“靜”;
三是在各類“靜態圖形”中運用相關的知識和方法(如方程、相似等)進行探索,尋找各個相關幾何量之間的關係,建立相應的數學模型進行求解。
轉載請超鏈接註明:頭條資訊 » 能考上重點高中的學生,不僅會做這類題,而且還做得不錯
免責聲明
:非本網註明原創的信息,皆為程序自動獲取互聯網,目的在於傳遞更多信息,並不代表本網贊同其觀點和對其真實性負責;如此頁面有侵犯到您的權益,請給站長發送郵件,並提供相關證明(版權證明、身份證正反面、侵權鏈接),站長將在收到郵件24小時內刪除。