大家好!今天和大家分享2道國外的初中數學競賽題。一道是日本數學競賽題,一道是印度初中數學競賽題,這兩道題都是化簡二次根式的題目。不少國內學生看後表示,難度不大,只是基礎題而已。
下面我們一起來看一下這兩道題目。

先看這道日本的競賽題。
這道題實際上考查的是分母有理化,所以只需要在分子分母同時乘以分母的有理化因式即可。但是分母由3個數字組成,它的有理化因式也有很多個,如果一個個試那就太麻煩了,所以先觀察一下分子。
分子是4√3,要想把分子約掉,分母也要出現√3的形式,那麼很明顯分母的有理化因式就是2+√3-√7。
找到有理化因式後,分子分母同時乘以有理化因式,然後再將分母用平方差、完全平方公式計算出來,分子先不計算,然後再對分子分母進行約分即可得到答案。
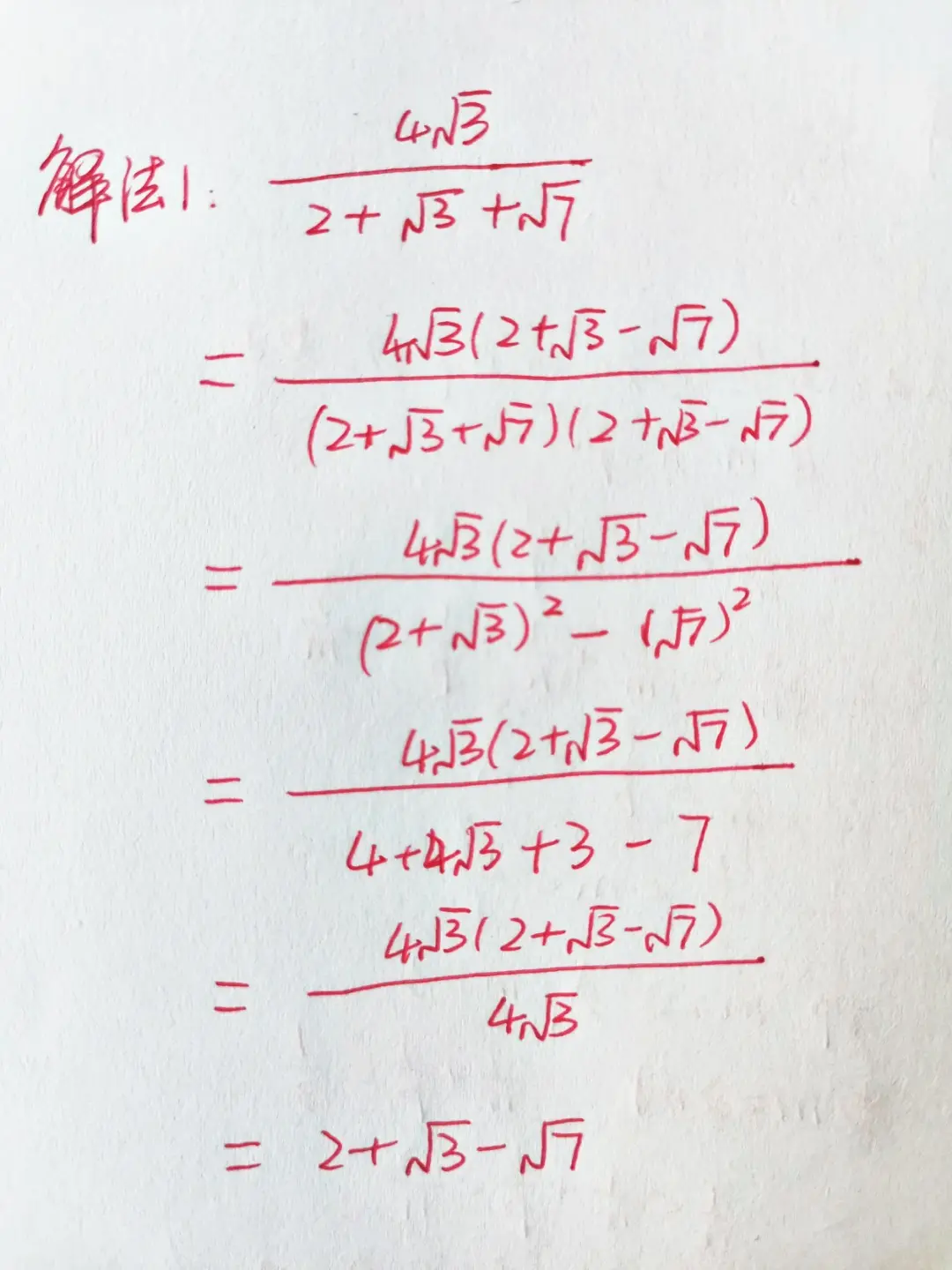
上面這個方法比較簡單,也比較容易理解。不過也有同學表示,不從分母而是從分子入手也是可以的。從分子入手確實沒有問題,但是需要對數字一定敏感度,才能解出來,因為這樣需要用到添項法。
因為4√3=7+4√3-7=4+4√3+3-7=2²+2×2×√3+(√3)²-(√7)²=(2+√3)²-(√7)²=(2+√3+√7)(2+√3-√7),然後再約分同樣可以得出答案。
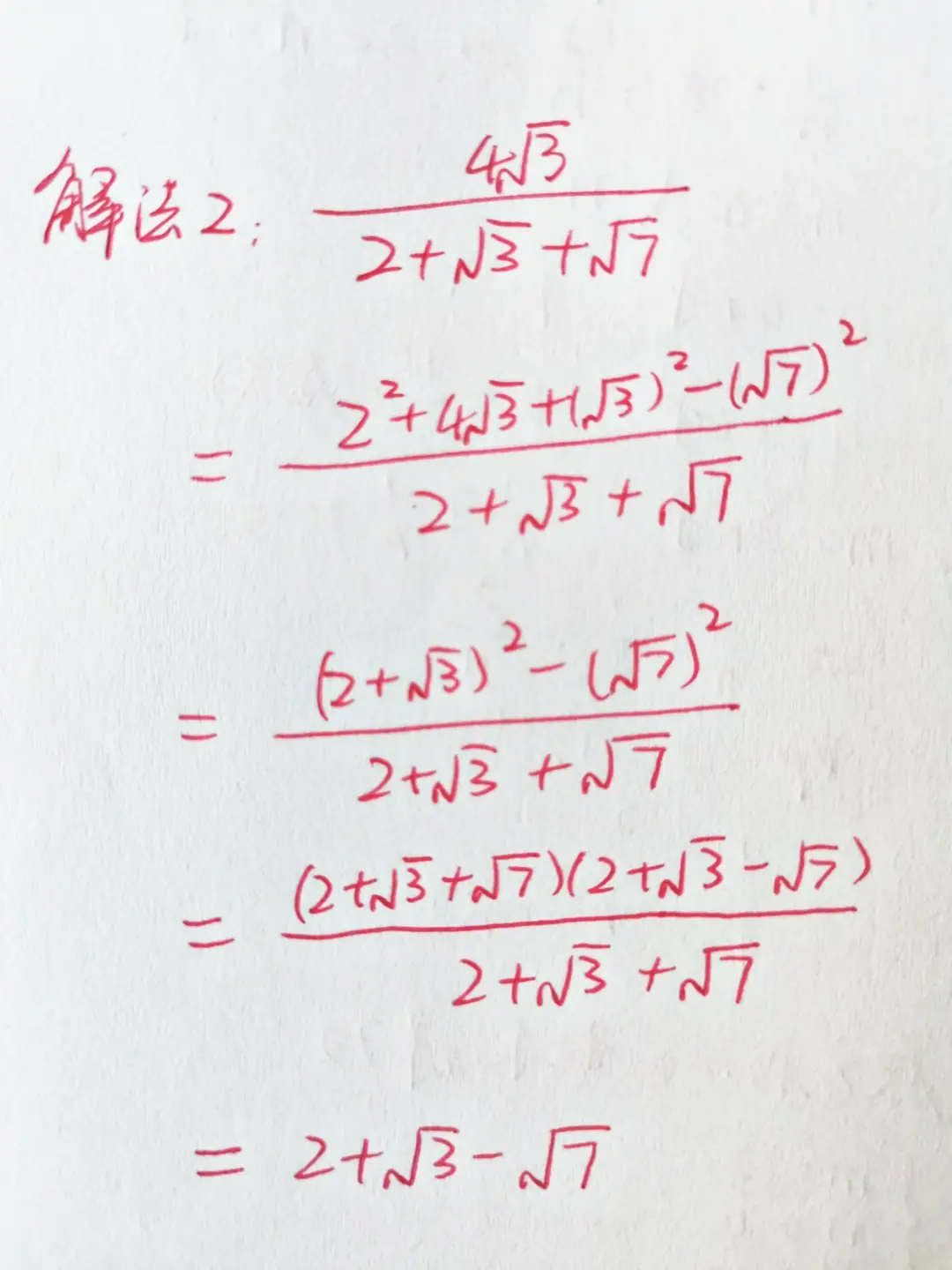
這道日本競賽題的難度確實不太大,但是第2種解法對學生的數字敏感度要求還是挺高,第1種解法更簡單,更容易想到,也是分母有理的基本方法。
看完日本競賽題,我們再來看看下面這道印度的競賽題。

這道印度競賽題從形式上看似乎比日本競賽題要難,畢竟數字更多。先來看一下形式,很明顯不可能直接將分子分母同時乘以分母的有理化因式,因為這樣的計算量將會非常大。
但是再觀察一下分母,如果將2√5寫成√5+√5,那麼分子分母就都是四個數字,數字多那麼可以想到進行分組。顯然,分母可以分為√3+√5和√5+√7兩組,分子是否也可以這樣分組呢?
在分子中,將√15和5提一個√5出來,就剩下√3+√5,將√21和√35提一個√7出來,剩下的也是√3+√5,然後再提出√3+√5,就可以將分子分解成(√3+√5)(√5+√7)。
到了這一步,可以將分子分母同時除以(√3+√5)(√5+√7),然後再對分母中的分數進行有理化即可得到答案。
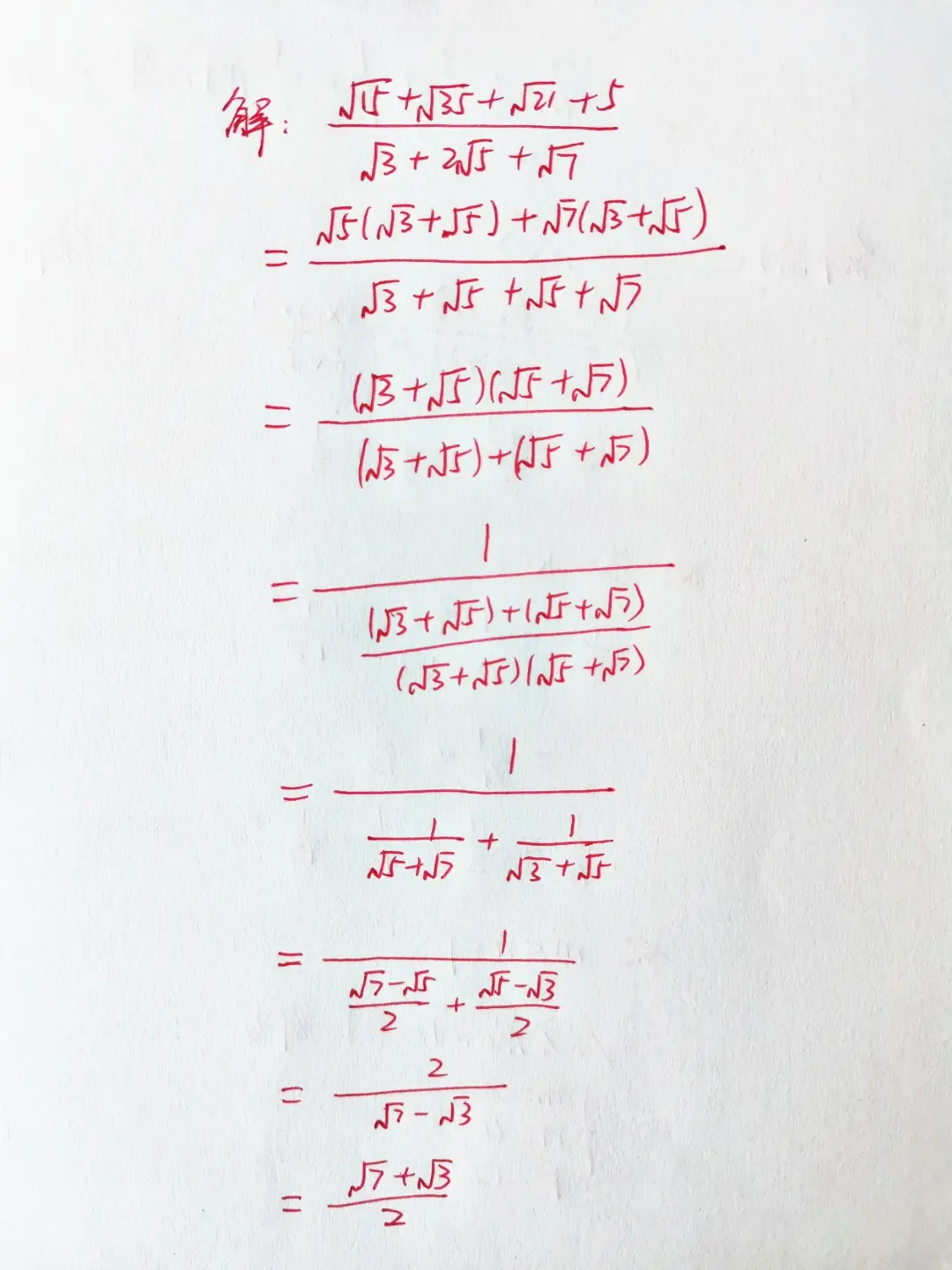
當然,在對分子進行因式分解後,也可以先求出這個式子的倒數,再求最終的值。
這兩道競賽題的難度確實不大,國內初中生做起來並不算太難,所以國內學生覺得這就是基礎題。
轉載請超鏈接註明:頭條資訊 » 2道國外數學競賽題:化簡二次根式,國內學生:基礎題
免責聲明
:非本網註明原創的信息,皆為程序自動獲取互聯網,目的在於傳遞更多信息,並不代表本網贊同其觀點和對其真實性負責;如此頁面有侵犯到您的權益,請給站長發送郵件,並提供相關證明(版權證明、身份證正反面、侵權鏈接),站長將在收到郵件24小時內刪除。